有 topological insulator 的基础背景，最近 Weyl semimeral 很火，看了文章还有不少疑惑，希望能有专门搞这个方向的大神解释一下。非常感谢！

发现好久都没有人回答。。。由于蔽组有人做这个，本人对其略知一二，抛砖引玉吧。

• Fermi arc is simply a part of a Fermi circle (loop).
• Weyl semimetal has nondegenerate Dirac points in the 3D bulk, which are called Weyl nodes.
• Weyl semimetal has topologically protected surface states, which connect two Weyl nodes in the projected 2D surface Brillouin Zone ( parametrized by (|k|,\ heta) in terms of polar coordinates ).
• Let's assume the surface state is localized at either top or bottom surfaces. For some \ heta, the state is localized at the top surface. For the rest of \ heta, the state is localized at the bottom surface.
• This means, an entire Fermi loop is splitted into two parts localized at the top and bottom surfaces. Each part is a Fermi arc.

不是做这个方向的，对这个东西大致懂一点。

Dirac semimetal是时间反演和空间反演保护的，破时间反演或空间反演有就可能在倒空间得到分立的一对手性相反的weyl points。这就是常说的weyl semimetal。

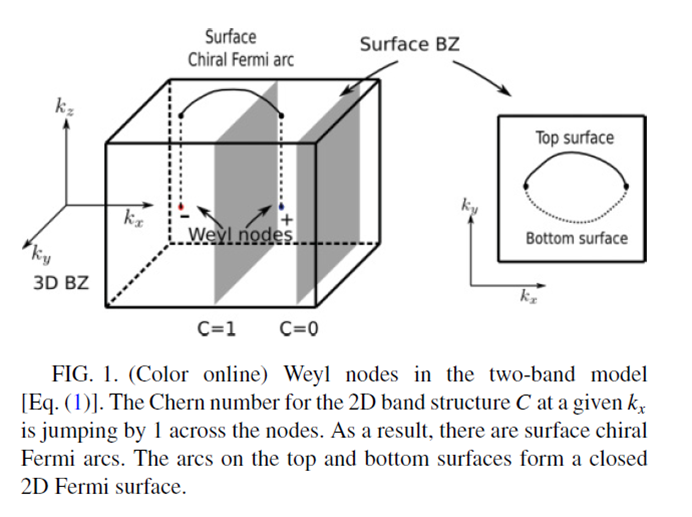
Fermi arc指的是Fermi面与表面布里渊区的交线（排除特殊情况，表面与一对Weyl points 连线垂直，Fermi arc消失）。通常在一般的材料中，这样的交线是一个闭合的曲线，而在weyl semimetal中交线是一段弧，称为Fermi弧。

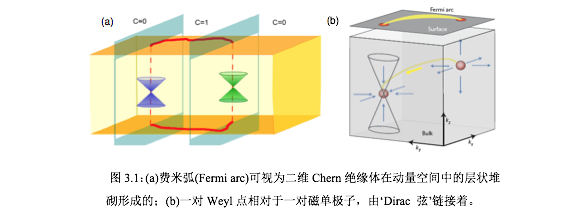
Fermi弧的成因是这样的。对三维体布里渊区切片，当切片穿过weyl points连线时，二维切片可以得到一个非零的Chern number，对应于一个反常量子霍尔态。如图。

Phys.Rev.B 84, 075129

反常量子霍尔态有表面态，在表面布里渊区内，费米面与所有这些表面态的交线就构成Fermi弧，起止于一对具有相反手性的Weyl points。

1. Weyl semimetal 概念

首先要是一个semimetal，semimetal的定义个人认为可以这么定义：满足以下两个条件的材料都可以被称为semimetal，a, 必须有费米面（哪怕只是几个点）; b, 费米面上electron pocket和hole pocket的里包含的粒子数刚好抵消。

其次在费米面附近有Weyl点（也就是导带和价带的交叉点，必须是二重简并交叉点）。或者说electron pocket或者hole pocket中包含了Weyl点。如果是个理想的Weyl semimetal，那么费米面刚好穿过Weyl点。

2. 在有Weyl点的体系中，当费米面穿过Weyl点是，会有Fermi arc连接两个不同手性的Weyl点。如果费米面没有穿过Weyl点，那么也就看你的费米面包含了几个Weyl点，费米面中所包含的Weyl点的Chirality总和为N的话，那么从这个费米面上会穿出N条Fermi arc出来。

3. 实验上看到了Fermi arc不代表这个体系有Weyl point。 只有连接了两个孤立electron pocket或者是hole pocket的Fermi arc才能证明在这两个pocket之间必然存在Weyl点。 比如WTe2和MoTe2的Fermi Arc就不能说明什么问题，因为那个ARC链接的并不是两个孤立的pocket。

Weyl semimetal态存在的证据有两个，都是独立的，一个是bulk state里存在Wely cone，一个是surface state里存在fermi arc。这些都可以用ARPES测出来。当然，会有人质疑，你怎么就能确定这个是fermi arc，而不是一个loop，这个可以利用它随能量的变化趋势，或者它与封闭曲线的交点是否是奇数来判断,具体的可以看xusuyang15年science或者物理所nature physics的文章。

------Yiming Pan (枫林白印)（原创，转载请注明出处）

“Weyl 半金属是一种在未来可能极具应用价值的光学材料。”

这篇介绍文章的第一句话，也是我个人对拓扑半金属领域的一种展望。作为一个凝聚态理论物理方向的研究者，不同于实验工作者把物理理论作为解释物理实验以及数据的一种图像或者拟合手段，我们看待物理理论更多的是建立一个概念，一个概念的建立可以是出于实验的需求，也可以是出于个人的灵感，或者是解方程时一种辅助工具或无奈妥协等等。我研究 Weyl 半金属的初衷便是如此，实际上是出于对手征反常[1-8]这个概念的好奇，一方面很好奇手征反常的物理根源，以及它涉及的其他物理概念(和数学上几何概念等)如手征对称性[9,10]，量子反常[8]，磁单极子[11,12]和指标定理[4-6]等，另一方面手征反常这种量子效应如何才能在实验上被观测到，它预言的那些反常效应(如手征泵浦效应，反常 Hall 效应，手征磁电流效应等)能否真的在材料中实现[13-15]。这些让人好奇的问题，我们都会再之后的章节讨论，但是在调研过程中突然意识到一个关于手征反常的“研究空白”。而这个研究“空白”就是 Weyl 半金属材料的光学性质很少被关注。

手征反常会给 Weyl 半金属材料中 述光学传播的 Maxwell 方程 供一个Chern-Simon 拓扑项[13]， 也就是场论中 axion 电动力学(axion electrodynamics)。 按照 Frank Wilczek 的 法[16]，我们给出 Axion Maxwell 方程组

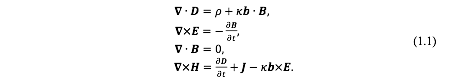
其中参数 ，b 是相空间中一对 Weyl 点之间的动量差，换句话说 代表轴子场。首先我们注意到上面第一个方程和第四个方程除了正常的电荷 和电流 ，还存在由轴子场 的散度贡献的反常电荷 和反常电流项 。 因此在无电荷源也无电流源的情况下，这个方程组也是非平庸的。比如在 WEM 中由于手征反常 项，可以导致光学的 Kerr 和 Faraday 旋转效应[17,18]。如果进一步把 Weyl半金属做成波导结构，并研究其波导模式传播的特征，我们就会发现这个 Weyl波导中的模式非常复杂，不同的光学模式(TE/TM 模)必然地会相互耦合起来，形成一种杂化模(hybrid mode)[19]。其次，由于 Weyl 半金属非平庸的 Dirac 型能带结构，它的光学响应也是比较特殊的。Weyl 半金属线性色散类似于 graphene，它的等离激元模式也与石墨烯类似，但不同于普通的金属。如果考虑不同 Weyl点对电磁波的耦合作用(谷间跃迁和谷内跃迁)，我们就会发现非局域的电磁响应[20,21]，双折射现象[18]和光学二象性[13,22]等。实验上也开始陆续关注 Weyl半金属中一些特别的光学信号如光电导，Raman 谱等[23-25]。

简而言之，Weyl 半金属中的手征反常给我们凝聚态领域 供了一类材料去研究 axion Maxwell 方程[16]。Weyl 半金属的在光学方向上的研究，可把它们大致分成三个方向:一是基于能带结构的传统的光学测量，这方面可以借鉴graphene 的光学研究手段，目标一方面是积累 Weyl 半金属的各类光学响应的数据，另一方面是希望借助光学的手段分辨出不同 Weyl 点的手征性来，这方面的理论构想也已经有报道[26,27]。二是实现三维 Weyl 光子晶体，这个领域如今非常活跃，把拓扑绝缘体做到光子晶体结构中去，实现拓扑光子学和非平庸的光学上单向传播的边缘态。至于三维 Weyl 光子晶体，最早是由 MIT 的 Ling Lu 等人在实验上实现了[28,29]。而基于这种类似光子晶体的进一步深入研究也在拓扑光子学领域进行着。三是基于手征反常的 Weyl 半金属表面等离激元以及各种几何 结构的光栅或波导(平板或脊型)的吸收损耗和模式分析等，这方面的研究进展缓慢，其中主要的原因还是手征反常效应太弱，虽然 Weyl 半金属材料已经积累不少，但是能够真正拿来作光学材料进行研究的，还是存在诸多限制。

• 什么是 Weyl 半金属?

回答这个问题，什么是 Weyl 半金属?我们从 Dirac 方程说起。从数学形式 上看，研究非相对论情况下的电子运动出发点是 Schrodinger 方程，比如将晶格的周期性引入方程中就能够获得固体能带结构，从而建立的能带理论，得到了金属，半导体以及绝缘体的分类。然而相对论极限下电子速度接近光速 c 能标达到GeV，固体中的电子根本达不到这么高的能量，因此早些年研究相对论情况下的 Dirac 方程其实就变成了粒子加速器的‘专利’了。从粒子物理的角度，如何加速电子，如何让粒子在加速器中获得更高的能量，就变成这个领域非常核心的问题。

不同于粒子物理需要更高能标的电子等，固体理论方向的发展却朝着完全低能的方向进行着，核心的原因非常简单，那就是固体材料的物性(力热光电磁等)基本由费米面附近(~eV)的(准)粒子激发决定。因此，各种低能有效模型应运而生，非常好地 描述各种材料体系的物性特征。

具有讽刺意味的是，凝聚态中的有效低能模型竟然也可以用 Dirac 方程来描述。这使得人们认识到研究相对论极限下的物理并不一定非要加速粒子到光速，比如石墨烯中 Dirac 点附近的电子激发就是相对论性的[30,31]，其费米速度(~106m/s)只是光速的 1/300。因此不同于粒子物理在越来越庞大越来越昂贵的加速器中寻找基本粒子，凝聚态则另辟蹊径地在固体材料中找各种类似基本粒子激 发。需要说明的一点是，维护粒子物理正统性的学者或者会认为凝聚态中相对论性粒子激发不过是一种“模拟”，并不是真实的基本粒子，只是满足相同的运动方程而已。然而我对这种观点却并不认同，因为材料中的相对论的粒子激发同样地真实，与粒子物理中的粒子不同，只不过是能标不同罢了。用更现代的重整化群观点来看[32,33]，不论是所谓的高能基本粒子还是费米面附近的准粒子都是在不同能标下的有效激发，比如在一个低能标下的基本粒子质子激发在另一个更高能标下则是由更基本的粒子夸克所组成的，粒子的‘基本性’是相对于能量尺度而言的。

为了满足相对论色散而构造了 Dirac 方程来 述相对论情形下的粒子行为，具体到不同的表象下，Dirac 方程可以给出多种费米子的激发如无质量的 Dirac费米子，Majorana 费米子和 Weyl 费米子[34]。有趣的是后面的 Majorana 费米子和 Weyl 费米子并没有在粒子物理中找到，但却在凝聚态中得以实现。Majorana费米子是一种‘反粒子既是它本身’的费米子，不带电荷，因此很难用电荷输运的实验手段进行测量，在凝聚态中实现 Majorana 费米子的激发需要等效的 p-wave 超导配对才行，另一方面还需要将自旋 Kramer 简并打破才能产生孤立的Majorana 费米子拓扑激发。如何实现 Majorana 费米子激发的模型非常多，如Kitaev 模型等，可以参看 Alicea 等综述文章[35,36]。Majorana 费米子巨大应用潜力在于实现拓扑量子计算和其辫子群的代数结构，如今如何在实验材料上找到Majorana 费米子以及怎样实现两个 Majorana 费米子辫子群交换依然是个非常热门的前沿课题。 H. Weyl 是一位德国物理学家和数学家[37]，其研究风格不同于 Einstein 的深邃简单也不同于 Heisenberg 的神秘诡辩，但和 Dirac 倒是风格接近，兼顾物理和数学之美。H. Weyl 从数学结构上 出，当 Dirac 方程中质量项消失后会有一种新的粒子出现，这种费米子带电荷，但无质量，成对出现。但后来 Weyl 失望地发现这种粒子破坏 parity 对称性，这在当时被认为是所有基本粒子都必须满足的一种‘硬性’对称性。随着粒子物理的发展越来越多的粒子被预言并发现，人们进一步猜测 Weyl 费米子可以用来描述无质量的中微子(neutrino)，但是后来实验发现中微子振荡并证实中微子有质量[38]。可惜，Weyl 费米子从数学上被提出来，在物理学中转了一圈，随后又回到数学领域中去，而在粒子物理中则被束之高阁了。

但美好的事物总能找到其栖身之所，Weyl 费米子亦是如此。Weyl 费米子经过凝聚态理论物理学家，计算物理学家，材料物理学家以及实验物理学家这些年接力棒似得不断尝试与找寻，终于在 TaAs 这一族非磁材料中找到了[39-43]，并在 2015 年被 Science，PRX，Nature Physics 以及Nature Communication 等期刊杂志广泛报道。对于 Weyl 费米子的材料实现过程，只谈 TaAs 材料未免太过单薄，容易让后来者以为这个材料是无意中发现的，也容易让人忽略掉其他科学家对此问题阶段性的重要贡献。因此我们简短回顾一下发现 Weyl 半金属 TaAs 材料的发展过程。

打从石墨烯中发现 Dirac 费米子激发开始，其实在凝聚态中做‘等效的基本粒子’的思路就已经打开了，因此从这个思路出发，可以很乐观地说找到 Weyl 费米子只是时间问题。从固体能带结构来看，Weyl 费米子出现在两个非简并的电子能带交叉时，交叉点叫做 Weyl 点，如图 Fig.1a 所示。在 Weyl 点附近的能带色散近似线性，这种能带结构的材料我们称之为 Weyl 半金属(semimetals, not half-metals)。一般在能带论中，能带交叉点很容易由于一个很小的扰动而打开一个能隙，使得交叉点消失。但是在三维情况下，比较特殊的是小的扰动不可能打开一个能隙，而只能使得Weyl点发生一点能量上的移动而已。因此可以说Weyl点是被保护着的，从而 Weyl 费米子的激发也是被保护的。

这个保护性可以简单地理解为:Weyl 半金属中两个能带产生了一个二能级系统，可以用 2×2Pauli 矩阵来 述 ，其 Hamiltonian 可以写成 。由于只有三个 Pauli 算子被用于 Weyl 半金属三个动量分量上了。任何其他引入的扰动项必然通过 Pauli 算子耦合进入系统，因此扰动项必然可以重新写成 ,也就是说能量零点发生了平移，但是Weyl点依然存在在 处。

另外一种理解这个保护性的角度是 Berry 相的拓扑非平庸性。我们对不同Weyl 点附近的 Berry 曲率 作一个面积分，并得到拓扑不变量(winding number) , 这个不变量可以叫做手征荷，一对正负相反的手征荷存于相空间中不同位置，就像一对正负磁荷相反的磁单极子一样。如图Fig1.1b 所示，可以看出一对拓扑非平庸的 Weyl 点是从拓扑平庸的相空间中相互分离出来的。换句话说，如果希望消灭掉一个Weyl点必须要用一个和它相反的 Weyl 点进行融合，并一同湮灭。

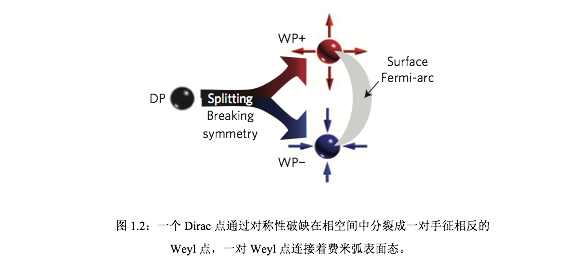
如何从 Dirac 半金属中得到一对 Weyl 点呢?这个问题我们已经很清楚了，Dirac 方程是 4×4 矩阵形式的，因此需要找到合适的扰动项(或者说质量项)使得 Weyl 点可以在相空间中分离开来，而不是像 Dirac 质量项那样打开 Dirac 点的能隙。4×4 矩阵形式的 Gamma 矩阵有很多，这个就有很多可选择的质量项，这是一个分类问题，需要在专门的章节讨论它。 从对称性分析知，Dirac 点是 四重简并的，也是手征性简并的，原因是由于时间反演对称性以及空间反演对称 性的要求。如果要将一个四重简并的 Dirac 点劈裂成两个手征相反的二重简并的 Weyl 点，就需要至少破坏时间反演或者空间反演对称性[44,45]，从而使得 Weyl 点在相空间中分离开来，并在单个 Weyl 点局域位置得到一个拓扑非平庸的 Weyl费米子激发，如图 1.2 所示。

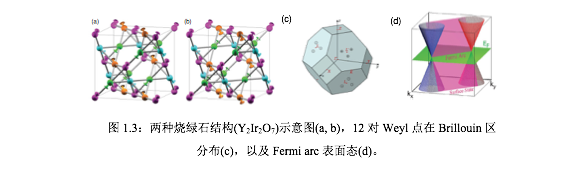
这样就开始了人们在材料中寻找 Weyl 半金属的旅程。首先使得 Weyl 半金 属引起极大关注的是由南京大学X.G. Wan在2011年提出的烧绿石材料中发现的Weyl半金属相[46],如图 1.3 所示。 其中“a，b图”是两种典型的烧绿石磁结构，c 图是烧绿石这类材料中被预言的 24 个 Weyl 点，非常丰富，同时他们还预言了Fermi arc 的存在。这一类烧绿石结构是磁性材料，通过破坏时间反演对称性来 实现Weyl半金属。但实验中却发现由于磁畴的存在在材料难以获得并且由于磁 性对光电效sul应的影响较大，不利于ARPES表征能带结构。

这期间人们转而求其次，首先实现三维Dirac半金属然后再想办法进一步获得Weyl相，因此类似3D Dirac半金属材料被第一性原理计算方法广泛预言，其中比较具有代表性并被ARPES实验证实的3D Dirac半金属就是Cd3As2[47]和Na3Bi[48]，关于这两个材料相关实验报道也非常多[49,50]，我们也会在讨论Weyl半金属输运性质时涉及。另外一个3D Dirac半金属材料是Bi1-xSbx合金[51]，当x大约为3%之时，Bi1-xSbx合金经历一个从拓扑绝缘体到普通绝缘体的一个量子相变，而处于拓扑相变点时能隙刚好闭合，并给出一个无质量的Dirac费米子的激发。上面提到的三个材料中的Dirac费米子在外加磁场的环境下都会通过破坏时间反演对称性得到Weyl费米子的激发。

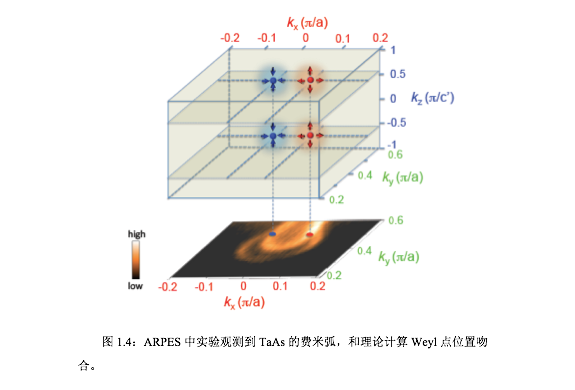
既然引入磁性难以在实验上进行测量，那么如何在非磁材料中找到破坏空间反演对称性的材料便成了一个新的探索方向。而在2014年底中科院[52]以及Princeton大学[53]两个小组几乎同时预言TaAs族结构中包括TaAs, TaP, NbAs, NbP四个材料就是这样一类非磁的Weyl半金属材料，并且很快被世界上各个实验小组相继证实。如图所示1.4，为TaAs族材料的典型结构以及ARPES中观测到的费米弧表面态。至此，Weyl半金属以及Weyl费米子在凝聚态领域大火了一把，并成为2015年度科技类一大新闻事件，而被广泛关注。

在回顾Weyl半金属这个发展过程时，我们关注点在于Weyl半金属如何一步一步被实现的大趋势，而不是具体到某位学者或者某个团队或者某篇文章上面。当然必须承认的是这一领域的发展，在一些重要时刻都是有一些特别重要的科学家或者研究小组的工作的贡献。但从大的趋势上看，有趣的是， Weyl半金属的发展，似乎是它自己在凝聚态的土壤中自发生长出来的一样。而且这个领域的发展还进一步催生许多新的意料之外的成果，接下来就来零星地归纳其中一些。

• 新型拓扑Weyl半金属

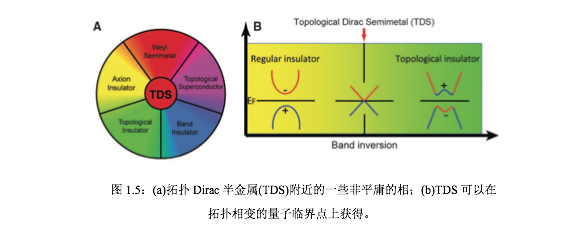
Weyl半金属作为一类拓扑Dirac半金属，和它临近的拓扑相可以分出好多种来。这些相就在Weyl半金属相的旁边，稍稍调整系统参数，那么就会进入一个其他相[49]，如axion绝缘体，拓扑绝缘体，普通绝缘体和拓扑超导体等，如图1.5a所示。而实际上如拓扑绝缘体或者拓扑超导体本身也可以进一步细细分类，得到更多的子相。如图1.5b所示，则说明拓扑Dirac半金属可以看作是拓扑相变临界点时的一个特殊相，介于普通绝缘体和拓扑绝缘体之间如Bi1-xSbx合金(x=3%)[51]或者加压（参杂）下HgTe[44,45]。

而且就Weyl半金属这个相来看，细分下来，也并不唯一。因为我们已经发现如第一类Weyl半金属（HgTe, TaAs族等），第二类Weyl半金属（WTe2等）[56-58]，Double-Weyl半金属（HgCr2Se4, SrSi2等）[59-61]以及Nodal-line半金属（Cu3NZn(Pd), Pb(Tl)TaSe2,Ca3P等）[62-65]。关于这些Wey半金属相的分类过程，在第五章中进行了专门的讨论，这儿就简单介绍一下他们的异同。

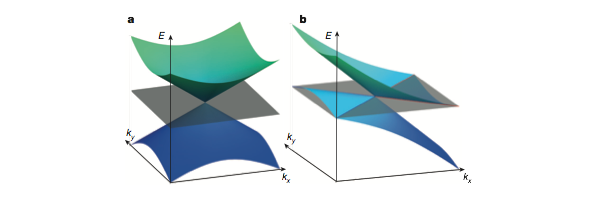
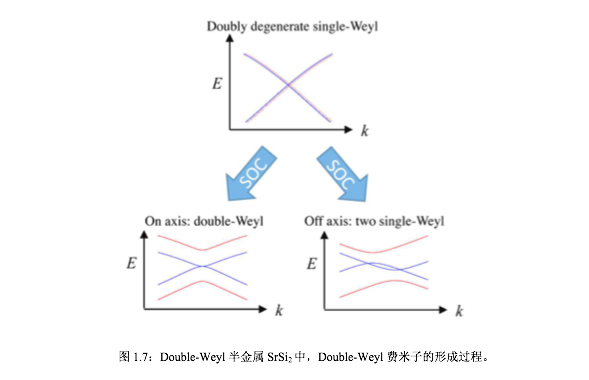
首先所谓第一类或者第二类是为了讨论WTe2材料中的一种特殊情况而定义出来的。如图1.6所示，a图为第一类WSM,也是通常认为的能带结构，b图为第二类WSM，这是一类能带发生扭曲倾斜的一种Weyl半金属，最大的特点就是调节费米面的时候，导带和价带也总会被切到。而Double-Weyl半金属最大的特点就是它的手征荷是而不是，同时在Weyl点附近的色散具有很强的各项异性，沿一个方向线性而沿另外两个方向上二次性。典型的产生过程如图1.7所示。在SrSi2材料中[60]，两个手征相同的Weyl点由于自旋轨道耦合(SOC)退简并一次，并在‘在轴’(on-axis)条件下下形成double-Weyl费米子能带，类似于双层石墨烯形成平方接触的色散过程。

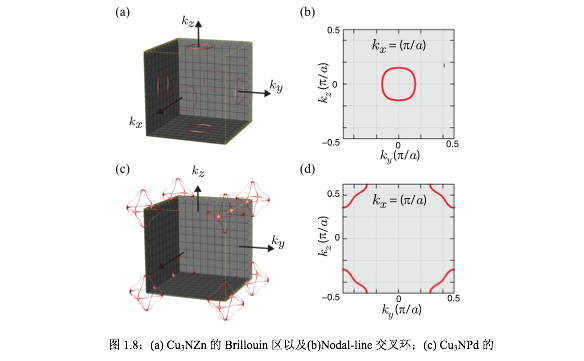
还有一种半金属材料，它的能带交叉不是点接触式，而是线接触式，交叉点形成一个闭合线性，这种材料称之为Nodal-line半金属[62,66]。如图1.8所示，为理论计算得到的Cu3NZn(a和b图)，Cu3NPd(c和d图)。从场论中看，Nodal-line半金属本身对微扰很敏感很容易打开能隙，并不具有拓扑保护特性，但是实验材料中由于晶体对称性的保护，在高对称点抑制微扰的产生，使得Nodal-line激发得以存在。我们可以把Nodal-line半金属中的线接触交叉过程，看作是直径上的一对Weyl点在相空间中画圆并连成一个闭合环状。同样地，一对Weyl点在材料表面会形成费米弧，那么对于Nodal-line半金属，这样的费米弧会在闭合环内彼此交织并最终形成一个鼓状的表面flat band（平带）[62,63]，这种鼓状表面平带的边缘固定在交叉点环上。这种奇特的表面态物性尚不清楚，目前已引起人们的极大的热情与兴趣。

这些Weyl半金属中非常规的拓扑相的研究，正在有条不紊地开展着。虽说Weyl费米子的想法来源于粒子物理，但是当这个领域一旦发展起来，又会更进一步提高并拓展我们对Weyl费米子的认识，这样的案例在科学的发展中已不胜枚举了。

• Weyl半金属的实验‘指纹’特征

我们并不打算在这儿过多的讨论Weyl半金属的各种有趣的特征，因为我已经在PhD论文中仔细分析它们，如chiral anomaly, chiral magnetic effect, anomalous Hall effect, chiral pumping, negative MR, Fermi arc, Large unsaturated MR 等等。从实验上如何判断一个材料就是Weyl半金属，这个问题是我想要在此交代的。我们知道Weyl半金属可看作是一种‘三维石墨烯’，是二维石墨烯的一种三维拓展，而Weyl半金属本身拓扑性质早在拓扑绝缘体的研究中被人提出了，因此Weyl半金属的性质并不新鲜，这样的观点现在依然盛行，虽然我并不尽认同。因此早些年关于它的研究被人搁置而小众化。

就个人的观点来看，Weyl半金属中最重要的概念应该是手征反常(chiral anomaly)。手征反常是石墨烯同时也是拓扑绝缘体中所没有的一个量子反常现象。手征反常是Weyl半金属中众多奇异电学输运和光学现象的诱因。对于Weyl半金属材料来说，它目前实验数据积累的方向主要集中在三点上：一是电场磁场平行时，各项同性的负磁阻现象[13]，这个可以视为手征反常诱导的输运特征之一；二是电场磁场垂直是，不饱和的类线性磁阻效应[67]，这个物理机制现在还没有定论，但是应该和线性色散的能带结构有关；三是ARPES中观测到的费米弧表面态以及Dirac cone体态，这是最直接的‘指纹’证据了[39-43]。然而对于判断一个材料是否是Weyl半金属，这些特征是需要交叉验证的。

特别地，对于像Double-Weyl半金属来说，是否能依然观测到它的负磁阻现象，还有一种情况如ZrTe5材料[68]，虽然实验上观测到的负磁阻现象但是理论预言它却并不是Weyl半金属相。同时，对于第二类Weyl半金属如WTe2等，它的费米弧表面态深埋在体带之中，想要在ARPES中找到费米弧并不容易(也已经出来相关实验报道)，另外第二类Weyl半金属的手征反常具有各项异性，只有沿着特定方向才会有手征反常效应，这会导致负磁阻的各向异性[56]，这也是很有趣的一件事情。最后，对于Nodal-line半金属来说，它的表面态是鼓状平带，不同于费米弧结构，另外输运方面的数据也尚无报道。

• 参考文献

1. Ioffe, B. L. International Journal of Modern Physics A 21.31 (2006): 6249-6266.
2. Gozzi, E., D. Mauro, and A. Silvestri. International Journal of Modern Physics A 20.20n21 (2005): 5009-5035.
3. Nielsen, Holger Bech, and Masao Ninomiya. Physics Letters B 130.6 (1983): 389-396.
4. Fujikawa, Kazuo. Physical Review Letters 42.18 (1979): 1195.
5. Fujikawa, Kazuo. Physical Review Letters 44.26 (1980): 1733.
6. Fujikawa, Kazuo. Physical Review D 21.10 (1980): 2848.
7. Nielsen, Holger Bech, and Masao Ninomiya. Physics Letters B 105.2 (1981): 219-223.
8. Banerjee, H. arXiv hep-th/9907162 (1999).
9. Buividovich, P. V. Physical Review D 90.12 (2014): 125025.
10. Kogut, John B. Reviews of Modern Physics 51.4 (1979): 659.
11. Rajantie, Arttu. Contemporary Physics 53.3 (2012): 195-211.
12. Hooft, Gerard. Nuclear Physics: B 79.2 (1974): 276-284.
13. Hosur, Pavan, and Xiaoliang Qi. Comptes Rendus Physique 14.9 (2013): 857-870.
14. Burkov, A. A. Journal of Physics: Condensed Matter 27.11 (2015): 113201.
15. Kharzeev, Dmitri E. Progress in Particle and Nuclear Physics 75 (2014): 133-151.
16. Wilczek, Frank. Physical review letters 58.18 (1987): 1799.
17. Kargarian, Mehdi, Mohit Randeria, and Nandini Trivedi. Scientific reports 5 (2015); arXiv:1503.00012 (2015).
18. Jackiw, Roman, and V. Alan Kostelecky. Physical Review Letters 82.18 (1999): 3572.
19. Talebi, Nahid. arXiv:1511.03479 (2015).
20. Rosenstein, B., H. C. Kao, and M. Lewkowicz.arXiv:1508.01604 (2015).
21. Ramamurthy, Srinidhi T., and Taylor L. Hughes. arXiv:1405.7377 (2014).
22. Hosur, Pavan, and Xiao-Liang Qi. Physical Review B 91.8 (2015): 081106.
23. Liu, H. W., et al. Physical Review B 92.6 (2015): 064302.
24. Sushkov, Andrei B., et al. arXiv:1507.01038 (2015).
25. Xu, B., et al. arXiv:1510.00470 (2015).
26. Yang, Shengyuan A., Hui Pan, and Fan Zhang. Physical review letters 115.15 (2015): 156603.
27. Jiang, Qing-Dong, et al. Physical review letters 115.15 (2015): 156602. arXiv:1501.06535 (2015).
28. Lu, Ling, et al. arXiv:1502.03438 (2015); Science 349. 6248 (2015): 622-624
29. Lu, Ling, et al. Nature photonics 7.4 (2013): 294-299.
30. Ando, Tsuneya, Alan B. Fowler, and Frank Stern. Reviews of Modern Physics 54.2 (1982): 437.
31. Sarma, S. Das, et al. Reviews of Modern Physics 83.2 (2011): 407.
32. Wilson, Kenneth G. Reviews of Modern Physics 47.4 (1975): 773.
33. Shankar, Rev. Reviews of Modern Physics 66.1 (1994): 129.
34. Peskin, Michael E., and Daniel V. Schroeder. An introduction to quantum field theory. Westview, 1995.
35. Alicea, Jason.Reports on Progress in Physics 75.7 (2012): 076501.
36. Beenakker, C. W. J. arXiv:1112.1950 (2011).
37. https://en.wikipedia.org/wiki/Hermann_Weyl.
38. Bilenky, S. M., and S. T. Petcov. Reviews of Modern Physics 59.3 (1987): 671. And http://dayawane.ihep.ac.cn/twiki/bin/view/Public/
39. Xu, Su-Yang, et al. Science 347.6219 (2015): 294-298.
40. Xu, Su-Yang, et al. Nature Physics 11.9 (2015): 748-754.
41. Yang, L. X., et al.Nature Physics 11.9 (2015): 728-732.
42. Lv, B. Q., et al. arXiv:1503.09188 (2015); Nature Physics 11.9 (2015): 724-727.
43. Lv, B. Q., et al. arXiv:1502.04684 (2015); Phys Rev X. 5.031013 (2015).
44. Burkov, Anton. Science 350.6259 (2015): 378-379.
45. Bernevig, B. Andrei. Nature Physics (2015).
46. Wan, Xiangang, et al. Physical Review B 83.20 (2011): 205101.
47. Wang, Zhijun, et al. Physical Review B 88.12 (2013): 125427.
48. Wang, Zhijun, et al.Physical Review B 85.19 (2012): 195320.
49. Liu, Z. K., et al. Science 343.6173 (2014): 864-867.
50. Liu, Z. K., et al. Nature materials 13.7 (2014): 677-681.
51. Kim, Heon-Jung, et al. Physical review letters 111.24 (2013): 246603.
52. Weng, Hongming, et al. Physical Review X 5.1 (2015): 011029.
53. Huang, Shin-Ming, et al. Nature communications 6 (2015).
54. Rauch, Tomá?, et al. Physical review letters 114.23 (2015): 236805.
55. Ruan, Jiawei, et al. arXiv:1511.08284 (2015).
56. Soluyanov, Alexey A., et al. Nature 527.7579 (2015): 495-498.
57. Sun, Yan, et al. Physical Review B 92.16 (2015): 161107.
58. Chang, Tay-Rong, et al. arXiv:1508.06723 (2015).
59. Xu, Gang, et al. Physical review letters 107.18 (2011): 186806.
60. Huang, Shin-Ming, et al. arXiv:1503.05868 (2015).
61. Jian, Shao-Kai, and Hong Yao. arXiv:1503.07429 (2015).
62. Yu, Rui, et al. arXiv:1504.04577 (2015); PhysRevLett.115.036807
63. Kim, Youngkuk, et al. arXiv:1504.03807 (2015); PhysRevLett.115.036806
64. Bian, Guang, et al. arXiv:1505.03069 (2015).
65. Bian, Guang, et al. arXiv:1508.07521 (2015).
66. Burkov, A. A., M. D. Hook, and Leon Balents. Physical Review B 84.23 (2011): 235126.
67. Borrmann, Horst, et al. Nature Physics 11, 645–649 (2015).
68. Yuan, Xiang, et al. arXiv:1510.00907 (2015).
69. Yazyev, Oleg V., and Yong P. Chen. Nature nanotechnology (2014).

• Weyl半金属的实验数据

现在开始讨论Weyl半金属这个领域目前积累的最重要的实验数据，这些数据主要集中于ARPES中能带分析和低温测量系统(PPMS)的磁阻与Hall电阻等。ARPES可以看Weyl半金属的表面态费米弧(Fermi arc)[1-6]，而低温输运数据可以看到手征反常导致的负磁阻现象[7-15]，这两大特征是目前实验上判断一个材料是否是Weyl半金属的鉴别‘指纹’(fingerprints)。实验上也在寻找其他证据，如热学磁学光谱等数据，但是似乎都不太明显，无法体现Weyl半金属不同寻常之处，以及与其他传统金属的区别。

对Weyl半金属介绍得更直白些，特别是对于实验上去研究这个材料的读者来说，明白Weyl半金属最重要的三大特性将会使其研究更加有效益。Weyl半金属的这三个特征分别是线性色散(linear dispersion)，拓扑表面态费米弧(Fermi arc)和手征反常(chiral anomaly)。

第一是线性色散，特别是当费米面接近Weyl点(或者Dirac点)时，线性色散表现出相对论特征，并强烈地影响着系统的电磁以及热学的响应[16]，不同于正常的金属(平方色散)。我将其一般性的影响归纳为，

1. 线性色散材料的态密度(DOS)为 ，其中d为空间维度。这是Weyl半金属作为Dirac材料的共性，Dirac材料包含甚广d-wave超导体，石墨烯，和拓扑绝缘体(TIs)等。这个态密度会直接决定某些典型实验测量曲线的整体特征，比如热学上电子比热随温度的变化关系 ，在STM中测量的微分电导随偏压(bias)的关系以及在异质结中的隧穿电流随门电压(gate)的关系也是类似的。这些关系主要都是由费米面附近的态密度决定的，因此反之也可以通过这些实验测量判断态密度随能量的变化关系。
2. 在磁场下，Dirac Hamiltonian量子化之后形成的Landau能级具有平方根依赖关系 ，这个依赖关系不同于Schrodinger费米子对磁场线性依赖关系，可以导致两个与众不同的特征（对于3D材料而言，Landau能级中包含动量k_z依然是好量子数）。第一个特征是，对磁场平方根依赖的系统中具有极大的Landau能级间距或回旋能量 。例如对2维自由电子气体(2DEG)，一个实验室条件下典型的磁场强度B=10T相当于 ，而相对比于石墨烯来说， 。这也是对于Dirac材料为什么量子效应在很多温度下依然可以被观测到，如在石墨烯中甚至可以在室温下（300K）测到量子Hall效应[16]。第二个特征是，Dirac费米子具有第零个Landau能级，这个能级是完全（赝）自旋极化，它在2D系统中是局域的（E=0），在3D系统中是手征的 (~k_z)。第零个Landau能级在2D材料如TI表面或者石墨烯中都可以给出量子Hall电导，而在3D材料中如Weyl半金属中则可以给出反常Hall电导以及手征反常等。另外在量子极限下，电子的输运行为以及散射机制都强烈地受第零个Landau能级极化特征的影响。
3. Dirac材料中Hamiltonian需要Gamma矩阵来描述，而Gamma矩阵导致Dirac费米子隐含一个非平庸的本征的Berry相位，这个Berry相位可以导致背散射被抑制，以及弱局域化或者弱反局域化效应增强[16]。另外，考虑其他电子散射过程如杂质共振等，或者超导配对中也需要考虑Gamma矩阵的结构。

第二个特征是费米弧表面态，特别需要把它和体态区分开来。在拓扑绝缘体中，体带是带隙打开的，而表面态则是无能隙的，穿过体带的带隙连接导带和价带，当费米面处于带隙中，体系的物理主要由表面态决定，然后对于Weyl半金属来说，和拓扑绝缘体不同之处在于其体带和表面态都是无能隙的，因此不管你如何调节费米面体带和表面态会同时被切到并贡献（当刚好切到Dirac点时，理论上体带态密度为零可视为无贡献，但实际情况下在Dirac附近热涨落量子涨落等效应明显，体带也不可完全忽略）。那是否真的对区分体带和表面态的贡献毫无办法呢？不，办法是有的。体带和表面态最大的不同就是其维度了，对于Weyl半金属来说，如果被测物理量很好地依赖能带的维度(D=3 or D=2)，那么就可以从物理量的power law中判断出是体带还是表面态的贡献。

Weyl半金属Fermi arc表面态除了受体带拓扑保护之外，它的最大特征是其不连续性。它在二维表面动量空间中只存在于两个Weyl点在表面投影点之间(或者之外，穿过Brillouin区边界相接)，它起于某个Weyl点终于另一个手征相反的Weyl点，形成一段不连续的弧状等能面，因而得名‘费米弧’。费米弧的物理解释，可以把它看做是陈绝缘体在动量空间中的层状堆砌形成的[16,17]，如图3.1所示，关于这个问题的细节一会儿在推导出费米弧时再来细说。这儿给读者留下一个念想，就是说为什么会出现这种不连续的表面态费米弧呢？或者说这种现象在场论中是否有类似的对应物呢？那就是Dirac早年做电荷量子化[18,19]时提出来的Dirac弦，就是这么个类似的对应物。我们知道不同手征的Weyl点相当于动量空间中的一对磁单极子，按照Dirac电荷量子化的要求，磁单极子与反磁单极子之间必然存在一个Dirac弦连接彼此。类比之下可以认为，费米弧就是某种动量空间中的‘Dirac 弦’在表面的投影。这个类比的想法是非常有趣的，但是对此能否在实验上被证实也是怀疑的，因为从目前的情况看来，还看不出来为什么需要定义动量空间中的‘Dirac弦’这种东西，以及如何从实验上探测它。但是不管怎样，这仍然是个有趣的想法，留给读者去思考一番。

还是回到费米弧的实验测量上来。我们已经从角分辨光电子谱(ARPES)中得到明确的费米弧的信号特征，这些工作被不同组陆续发表在 science, nature physics 以及 physical review x 等杂志上了[2-6]。实验数据和第一性原理计算的数据吻合得非常之好，从而让人相当确认这些材料应该就是 Weyl 半金属了。当然，谨慎的人也不在少数，这种谨慎主要还是集中在输运上的负磁阻效应以及手征反 常上。这也反映一点，在 Weyl 半金属上实验积累的数据可能太单一了，缺少更多其他可信任的‘力、热、光、电、磁’方面的数据。还有一个问题可能会使得Weyl 半金属缺乏后劲，那就是不管是费米弧还是负磁阻都显得很‘无用’，它们虽然现象有趣但是目前看不出来应用前景，这个瓶颈如果不能解决，将会使得 Weyl半金属热度很快褪去，而同时对 Weyl 半金属的研究就会慢慢凋零，无法达到像石墨烯甚至拓扑绝缘体的热度。 第三个特征是手征反常，Weyl半金属的基础研究和应用价值也许可以从这个概念中开发出来。个人看法是手征反常才是Weyl半金属最与众不同的特征，可以区别于其他Dirac材料如石墨烯，拓扑绝缘体和d-wave超导等[16]，这也是为什么花费一整章来讨论手征反常的基本理论。但问题是，手征反常是一个量子效应非常微弱，怎么样在实验上观测它并不容易，如何利用这个效应则更是遥远的事情。然而事情并没有那么悲观，一方面已经陆陆续续发现其他更多的Weyl半金属材料（double-Weyl半金属， nodal-line半金属等）[20-23]，也许可以从这些新的材料中获得更强的手征反常效应，另一方面从光学测量上看手征反常相关的实验还在起步阶段，理论方面对于axion Maxwell方程的研究积累也很少，但是已经开始被人们重视起来了，这方面也许需要更多的光学研究者进入才能更快地搞清楚，如光学响应动态介电常数，表面等离激元, 波导模式等等。

手征反常在输运上可以导致负磁阻效应[24]和非局域输运行为[25]，而且也被相关实验测量所证实了。这个负磁阻效应，有很多办法推导出来，一会儿会给一个相对简单的推导结果。这儿必须交代两点，第一是这个负磁阻并非什么新的现象，其实就是已经知道的手征磁电流。虽然我们知道手征磁电流在平衡态下并不存在，但是在有平行电场磁场的条件下达到稳态的系统中，手征磁电流会通过一个手征电荷动态平衡过程贡献一个奇异的依赖于磁场平方关系的电导()，这个正向的电导在电阻上的表现就是负磁阻现象。第二点必须把负磁阻和其他正常磁阻有效区分开来。从实验上的磁阻曲线发现出三个特征，即在小磁场下出现弱反局域化，然后随磁场增加磁阻下降，视为负磁阻效应，最后在高磁场下磁阻重新增大，表现为正向的不饱和磁阻。在这一章中我们会分析弱反局域化和负磁阻现象的实验数据，但是不饱和磁阻则留在下一章专门来讨论。不饱和磁阻的理论基础，现在学界并没有一个统一的认识，不同组提出过好几个理论模型来解释之，加上这个不饱和磁阻现象也出现在其他并非Dirac材料如二维材料WTe2中，也导致现有的理论总是给不出一个直观的物理图像来。

最后还会提及由手征反常导致的非局域输运行为，如图3.2所示。这个想法最早是14年一篇PRX上提出来的[25]，最近则被复旦大学一个实验组在Cd3As2 纳米平板结构上实现了，这是个非常漂亮的实验[11]。同时，也期待更多类似的实验预言和实验数据的出现，这些对于理解并应用手征反常现象是非常有益的。

以上是我对Weyl半金属实验方面的一些整体看法，有些笼统又有些琐碎。因为这个领域正在发展中，也很难给出一个非常有见地的论述。对于想要涉足这个领域的读者来说，对于某些问题的认识不足以及对某些问题的担忧，则正是可能做出工作并有所建树的地方。

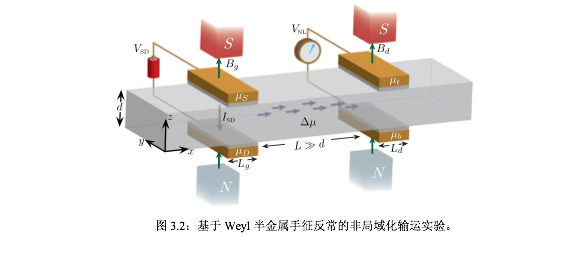
• 什么是费米弧？

现在来讨论Weyl半金属第一个鉴别‘指纹’——费米弧表面态。在讨论ARPES测量之前，我们用凝聚态中传统的方法从Weyl半金属的Hamiltonian来推导费米弧表面态的解析解来，虽然实际上可以用更加拓扑些语言来获得费米弧，而且随后也会涉及到。考虑一个Weyl半金属的Model Hamiltonian[26]，

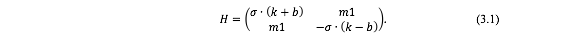
其中为Pauli算子。当Dirac质量项m=0时，左手Weyl电子的能量零点偏移到，而右手Weyl电子的能量零点偏移到b，总动量偏移量为2 。当 ≠ 0，左右手被混合起来了，但是只要 <|b|，则存在一支导带和一支价带会发生交叉，交叉点的位为 ，因此依然可以得到有效的Weyl费米子激发。上面的Hamiltonian是在动量空间中表达的，现在设 并考虑一个x=0的yz平面作为边界。为简单起见，用Heaviside阶跃函数来表示即 ，当x<0时为有质量Dirac真空而当x>0时为Weyl半金属体态。为了获得表面态解，求下面的Schrodinger方程，

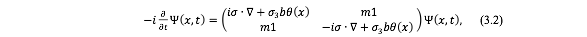
并注意到yz平面内的平移不变性，即沿着y和z反向的动量是一个好量子数，因此得到一个形式解 ，代入得到旋量场满足方程，

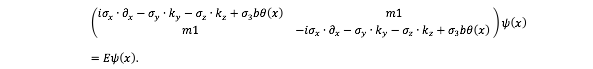
仔细分析这个方程，会发现只有 y 方向是完全与其他两个方向蜕耦合的，因此选择 0 1的本征值为+1 的本征态来化解这个方程的旋量部分，于是给出一个拟解为，

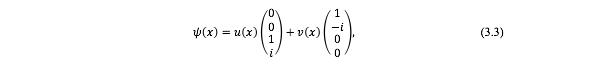
这个拟解导致色散关系=+ _y，同时函数 , 满足如下耦合微分方程组，

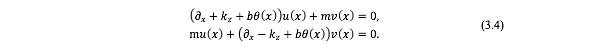
从上面的方程组中消去函数 ，得到关于函数 (x) 二阶微分方程

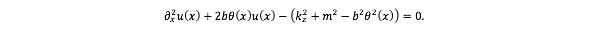
因此，得到

至此，代入形式解中，得到一个表面态解析解。我们来分析一下这个表面态解，首先这个量子态在x=0时向两边体系指数衰减，同时当x>0时为了使得量子态可归一化必然要求 ；其次表面态在yz平面满足平面波解对应于能量色散为 ，因此发现表面态色散其实也是手征的(chiral)；最后归一化条件给出对表面态解动量kz的限制条件，可以看出对于特定能量的表面态，等能面就是一段平行于Z方向的线段，线段的端点置于两个Weyl点的动量位置上，如图3.1a所示。这个直线线段就是所谓的费米弧(Fermi arc)，好像和我们一般见到的圆弧状并不相同，这是因为在具体晶格材料中需要考虑二阶项的贡献( )，这一项在解能量本征值时要求能量E依赖于动量，定性上分析得到一个有效的表面态色散为 ，这是个二次型的色散[26]。

接下来，我将给费米弧一个基于拓扑二维Chern绝缘体的理解[17]。通常期待费米面都会形成一个闭环(closed loop)，但是Weyl半金属却不是这种情况。有一个简单的方式理解费米弧的不连续性，那就是假设两个Weyl点分别处于动量 ，想象一个二维动量切面，比如xy-平面，那么在切面上就会形成一个二维绝缘体色散，现在让切面沿着kz方向运动，然后发现当切面穿过一个Weyl点时，其能带对应的陈数会发生一次改变。因此，动量切面在两个Weyl点之间都是二维的Chern绝缘体，陈数为C=1，而在Weyl点之外则是普通绝缘体，陈数为C=0。由于Chern绝缘体有一个手征的边缘态（即~k_y），因此所有介于两个Weyl点之间的动量切面堆砌在一起就形成一个表面态费米弧。换句话说，费米弧也不是什么稀奇的事情，不过是Chern绝缘体的边缘态在动量空间中的堆砌而已。

现在开始就TaAs为例介绍ARPES测量的数据[8,10]。不知道要不要先补充一下ARPES工作原理呢？算了，不了解ARPES的读者还是先去翻翻书吧，同时也随便把STM（扫描电子显微镜）以及光谱技术的测量手段也一并了解一下，因为在写这个论文时这些数据还没有出来，但相信很快Weyl半金属就会有STM以及光谱方面的实验被报道的。虽说并不打算具体讲解ARPES的操作过程，但是还是很有兴趣来比较这三种测量手段的优劣以及互补性。

首先比较ARPES和STM，ARPES的基本思想是利用光电效应，通过测量逸出电子的动能获得材料电子结构的信息，此外还利用了面内动量守恒，同时记录逸出电子的动能和动量，从而揭示电子能带色散关系。STM的工作原理基于量子隧道效应。当STM的金属探针和一个样品表面足够近时（0.1~1nm），两者之间波函数发生交叠，当外加一个偏压V时就电子就会在样品和针尖之间发生量子隧穿从而贡献一个隧道电流I。简单的理论分析可知，微分电导 正比于样品局域电子态密度，因此测量微分电导可以获取微观尺度下样品电子结构的实空间分布。对比ARPES和STM测量，就会发现它们一个是动量空间分辨的，另一个是实空间分辨的，这是两者的互补性，另外一点就是它们都是基于表面的电子测量，对样品极为敏感，因此对材料和实验条件的要求也非常苛刻。

而光谱技术是研究光与物质相互作用的主要实验手段，可能会在讨论Weyl半金属光学响应时涉及一些。它的测量技术有多种多样，但主要目的还是为了获得各种光学常数，如动态介电常数，复电导率等。在研究能带结构和准粒子动力学方面，光学探测和ARPES也有一定互补性。光学测量没有动量分辨信息(也没有STM实空间分辨能力)，得到的是不同动量方向总体贡献，但可以说它是频率（能量）分辨的；光学测量的是从占据态到空态的跃迁，包括带内跃迁和带间跃迁，能够提供电子能带费米面以上的信息，而ARPES测量的仅是费米面一下占据态的信息。此外光谱技术除了提供电子激发的信息，还能探测其他能够和光耦合的集体激发的响应，这为Weyl半金属的光学研究提供了实验手段。

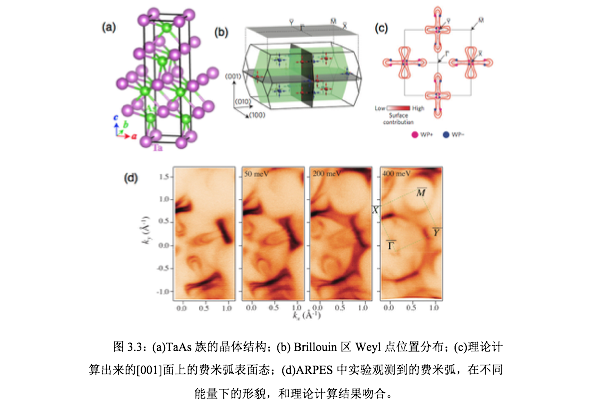
现在，就TaAs的ARPES来看Weyl半金属中的费米弧的实验图像上的特征[8,27]，如图3.3所示。其中a图是TaAs族典型的晶体结构，它的Brillouin区中包括12对Weyl点，其中4对空穴型(~-2meV)位于平面上而另外8对电子型(~20meV)位于Brillouin中心八个对称位置上（b图）。在c图中，我们看到费米弧表面态在三个位置，分别是, 以及和连线的中点位置，可以看出费米弧有两个特征结构，一个是蝴蝶结状另一个是圆角长方形状。而d图中显示的是ARPES在不同能量下的费米弧和计算的结果对比，非常吻合，详细分析参看文献[2-6]。另外，理论上关于TaAs族材料中国费米弧的spin texture以及SOC的影响分析，参看文献[28-30]。

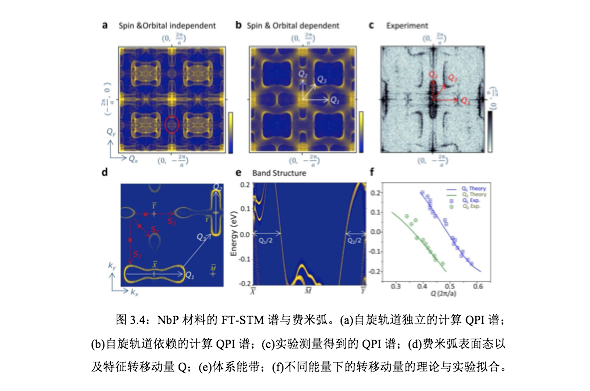
接下来，我们给出FT-STM的NbP材料的数据以及准粒子干涉(QPI)条纹分析结果[31-33]，如图3.4所示。我们发现数值计算出的Q空间态密度谱分布和实验测量获得的分布一致。特别地是有三个特征QPI转移动量Q1,Q2和Q3，它们分别对应于蝴蝶结状费米口袋内散射，圆角长方形状口袋内散射以及两个口袋间散射过程。至于S1,S2和S3散射过程则在实验上没有发现，如图d所示，主要原因在于STM测量的NbP表面没有这些散射存在，详细参看文献[32]。

参考文献

1. Balents, Leon. Physics 4 (2011): 36.
2. Xu, Su-Yang, et al. Science 347.6219 (2015): 294-298.
3. Xu, Su-Yang, et al. Nature Physics 11.9 (2015): 748-754.
4. Yang, L. X., et al. Nature Physics 11.9 (2015): 728-732.
5. Lv, B. Q., et al. arXiv:1503.09188 (2015); Nature Physics 11.9 (2015): 724-727.
6. Lv, B. Q., et al. arXiv:1502.04684 (2015); Phys Rev X. 5.031013 (2015).
7. Xu, N., et al. arXiv:1507.03983 (2015).
8. Huang, Xiaochun, et al. arXiv:1503.01304; Phys Rev X. 5.031023 (2015).
9. Xiong, Jun, et al. Science 350.6259 (2015): 413-416.
10. Zhang, Chenglong, et al. arXiv:1503.02630 (2015).
11. Zhang, Cheng, et al. arXiv:1504.07698 (2015).
12. Yang, Xiaojun, et al. arXiv:1506.03190 (2015).
13. Shekhar, Chandra, et al.arXiv:1506.06577 (2015).
14. Li, Hui, et al. arXiv:1507.06470 (2015).
15. Goswami, Pallab, J. H. Pixley, and S. Das Sarma. arXiv:1503.02069 (2015); Phys Rev B. 92.075205 (2015).
16. Wehling, T. O., Annica M. Black-Schaffer, and Alexander V. Balatsky. Advances in Physics 63.1 (2014): 1-76.
17. Hosur, Pavan, and Xiaoliang Qi.Comptes Rendus Physique 14.9 (2013): 857-870.
18. Polchinski, Joseph. Reviews of Modern Physics 68.4 (1996): 1245.
19. Bernevig, B. Andrei. Nature Physics (2015).
20. Yu, Rui, et al. arXiv:1504.04577 (2015); PhysRevLett.115.036807
21. Kim, Youngkuk, et al. arXiv:1504.03807 (2015); PhysRevLett.115.036806
22. Bian, Guang, et al. arXiv preprint arXiv:1505.03069 (2015).
23. Bian, Guang, et al. arXiv:1508.07521 (2015).
24. Burkov, A. A. arXiv:1505.01849 (2015).
25. Parameswaran, S. A., et al. Physical Review X 4.3 (2014): 031035.
26. Goswami, Pallab, and Sumanta Tewari.Physical Review B 88.24 (2013): 245107.
27. Weng, Hongming, et al. Physical Review X 5.1 (2015): 011029.
28. Lee, Chi-Cheng, et al. Physical Review B 92.23 (2015): 235104.
29. Sun, Yan, Shu-Chun Wu, and Binghai Yan. Physical Review B 92.11 (2015): 115428.
30. Xu, Su-Yang, et al. arXiv preprint arXiv:1510.08430 (2015).
31. Belopolski, Ilya, et al. arXiv preprint arXiv:1509.07465 (2015).
32. Zheng, Hao, et al. arXiv preprint arXiv:1511.02216 (2015).
33. Chang, Guoqing, et al. arXiv preprint arXiv:1511.02827 (2015).