- 手机:
- 18888889999
- 电话:
- 0898-66889888
- 邮箱:
- admin@youweb.com
- 地址:
- 海南省海口市玉沙路58号
g2o全称是:General Graph Optimization!所谓的通用图优化。
为何叫通用呢?g2o的核里带有各种各样的求解器,而它的顶点、边的类型则多种多样。通过自定义顶点和边,事实上,只要一个优化问题能够表达成图,那么就可以用g2o去求解它。常见的,比如bundle adjustment,ICP,数据拟合,都可以用g2o来做。
从代码层面来说,g2o是一个c++编写的项目,用cmake构建。它的github地址在:
https://github.com/RainerKuemmerle/g2o它是一个重度模板类的c++项目,其中矩阵数据结构多来自Eigen。
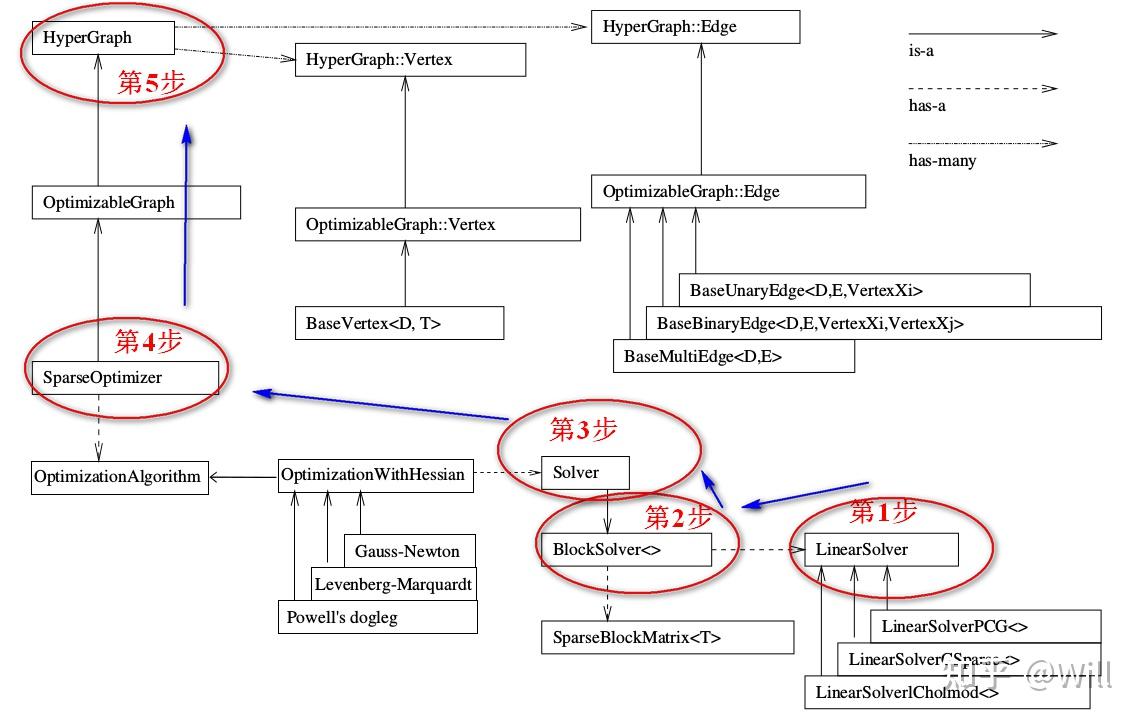
先看上半部分。SparseOptimizer是我们最终要维护的。它是一个Optimizable Graph,从而也是一个Hyper Graph。一个SparseOptimizer含有很多个顶点(都继承自Base Vertex)和很多个边(继承自BaseUnaryEdge, BaseBinaryEdge或BaseMultiEdge)。这些Base Vertex和Base Edge都是抽象的基类,而实际用的顶点和边,都是它们的派生类。我们用SparseOptimizer.addVertex和SparseOptimizer.addEdge向一个图中添加顶点和边,最后调用SparseOptimizer.optimize完成优化。
在优化之前,需要指定我们用的求解器和迭代算法。从图中下半部分可以看到,一个SparseOptimizer拥有一个Optimization Algorithm,继承自Gauss-Newton, Levernberg-Marquardt, Powell's dogleg三者之一(我们常用的是GN或LM)。同时,这个Optimization Algorithm拥有一个Solver,它含有两个部分。一个是SparseBlockMatrix,用于计算稀疏的雅可比和海塞;一个是用于计算迭代过程中最关键的一步
这就需要一个线性方程求解器。而这个求解器,可以从PCG, CSparse, Choldmod三者选一。
综上所述,在g2o中选择优化方法一共需要三个步骤:
- 选择一个线性方程求解器,从PCG, CSparse, Choldmod中选,实际则来自g2o/solvers文件夹中定义。
- 选择一个矩阵块求解器BlockSolver。
- 选择一个迭代策略,从GN, LM, Doglog中选。
G2O在数学上主要分为四个求解步骤:
- 定义顶点和边的类型,包括边(的计算误差和求导方式等)和顶点(的更新方式和边缘化);
- 构建图结构(添加顶点和边);
- 选择优化算法;
- 调用g2o进行优化。
在程序中的步骤为:
- 创建一个线性方程求解器LinearSolver。
- 创建矩阵块求解器BlockSolver,并用上面定义的线性求解器初始化。
- 创建总求解器solver,并从GN/LM/DogLeg 中选一个作为迭代策略,再用上述块求解器BlockSolver初始化。
- 创建图优化的核心:稀疏优化器(SparseOptimizer)。
- 定义图的顶点和边,并添加到SparseOptimizer中。
- 设置优化参数,开始执行优化。
typedef g2o::BlockSolver<g2o::BlockSolverTraits<3,1>> Block; // 每个误差项优化变量维度为3,误差值维度为1
// 第1步:创建一个线性方程求解器LinearSolver
Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>();
// 第2步:创建矩阵块求解器BlockSolver。并用上面定义的线性求解器初始化
Block* solver_ptr = new Block(linearSolver);
// 第3步:创建总求解器solver。并从GN, LM, DogLeg中选一个,再用上述块求解器BlockSolver初始化
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(solver_ptr);
// 第4步:创建终极大boss稀疏优化器(SparseOptimizer)
g2o::SparseOptimizer optimizer; // 图模型
optimizer.setAlgorithm(solver); // 设置求解器
optimizer.setVerbose(true); // 打开调试输出
// 第5步:定义图的顶点和边。并添加到SparseOptimizer中
CurveFittingVertex* v = new CurveFittingVertex(); //往图中增加顶点
v->setEstimate(Eigen::Vector3d(0,0,0));
v->setId(0);
optimizer.addVertex(v);
for (int i=0; i<N; i++) // 往图中增加边
{
CurveFittingEdge* edge = new CurveFittingEdge(x_data[i]);
edge->setId(i);
edge->setVertex(0, v); // 设置连接的顶点
edge->setMeasurement(y_data[i]); // 观测数值
edge->setInformation(Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma)); // 信息矩阵:协方差矩阵之逆
optimizer.addEdge(edge);
}
// 第6步:设置优化参数,开始执行优化
optimizer.initializeOptimization();
optimizer.optimize(100);
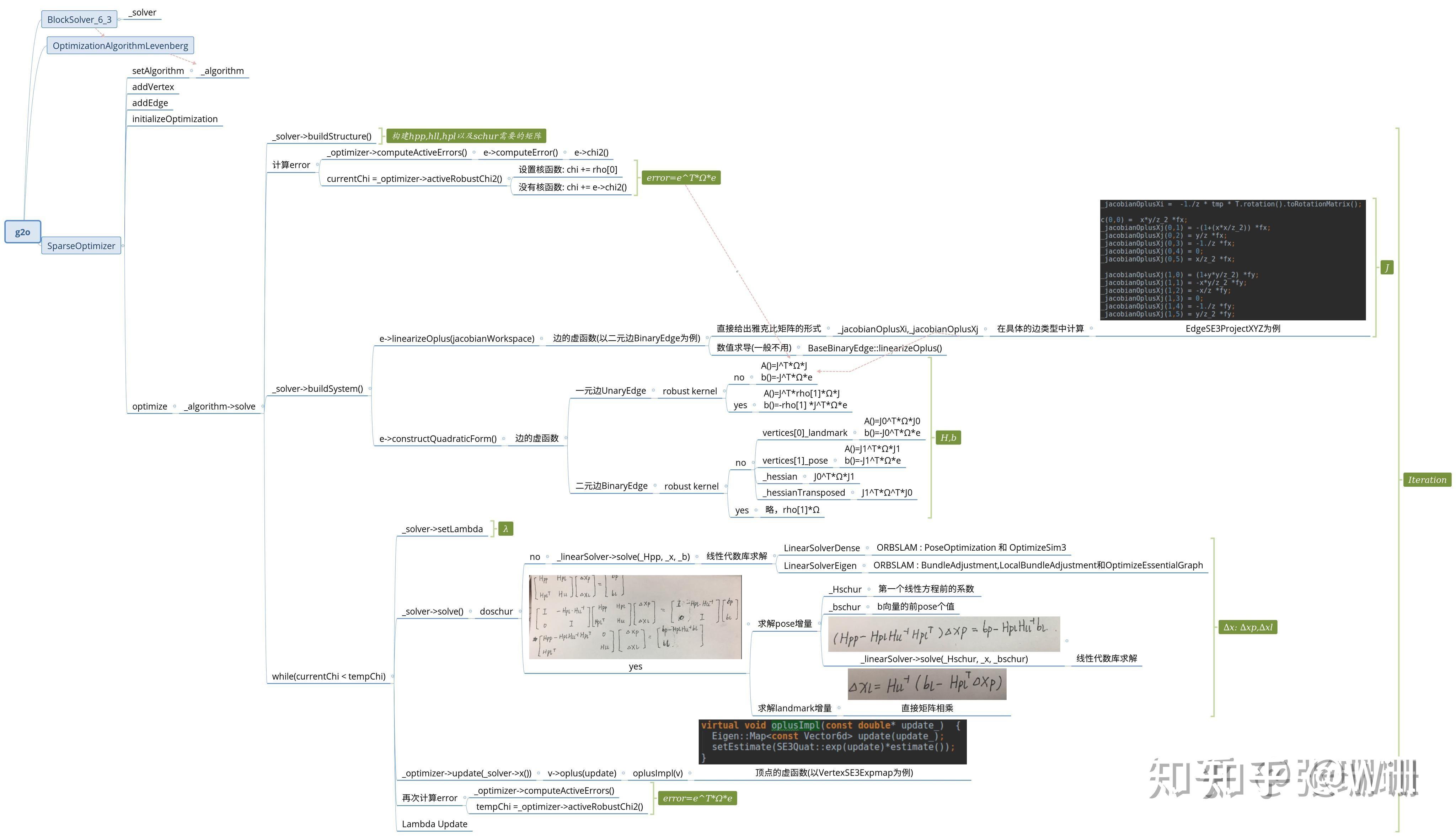
别人画的g2o的主要函数流程图:
参考:
张珊珊:g2o:非线性优化与图论的结合g2o::LinearSolverCholmod:使用sparse cholesky分解法。继承自LinearSolverCCS
g2o::LinearSolverCSparse:使用CSparse法。继承自LinearSolverCCS
g2o::LinearSolverPCG:使用preconditioned conjugate gradient法,继承自LinearSolver
g2o::LinearSolverDense:使用dense cholesky分解法。继承自LinearSolver
g2o::LinearSolverEigen:依赖项只有eigen,使用eigen中sparse Cholesky求解,因此编译好后可以方便的在其他地方使用,性能和CSparse差不多。继承自LinearSolver
求的线性求解器,完全采用第三方的线性代数库,主要采用Cholesky分解和PCG迭代,具体选择有:
1. Cholmod,CSparse(以上两者为比较著名的线性代数库)
2. PCG(pre-conditioner is block Jacobi)
3. Dense(dense Cholesky decomposition)
4. Eigen(sparse Cholesky decoposition from Eigen)
定义在core/block_solver.h中
template<int _PoseDim, int _LandmarkDim>
struct BlockSolverTraits //traits to summarize the properties of the fixed size optimization problem
_PoseDim表示位姿的最小流形维度,_LandmarkDim表示地标维度:
template<int p, int l>
using BlockSolverPL = BlockSolver<BlockSolverTraits<p, l>>;
定义了一些常用的BlockSolver结构,例如:
g2o::BlockSolver_6_3:表示pose是6维,观测点是3维。用于3D SLAM中的BA
g2o::BlockSolver_7_3:在BlockSolver_6_3的基础上多了一个scale
g2o::BlockSolver_3_2:表示pose是3维,观测点是2维
g2o::OptimizationAlgorithmGaussNewton
g2o::OptimizationAlgorithmLevenberg
g2o::OptimizationAlgorithmDogleg:Dogleg法(狗腿法)的推导与步骤-CSDN博客_dogleg算法
重要接口:
setAlgorithm()
addVertex()
addEdge()
addParameter()可以传入一些超参,比如相机内参
initializeOptimization()填入需要优化的subgraph或level
optimize()启动优化流程
1.调用所有边的linearizeOplus()函数,得到每个边的雅克比矩阵,然后把矩阵连接成一个大矩阵
2.调用所有边的computeError(),得到误差矩阵
3.基于雅克比和误差,使用优化器计算更新值△X(矩阵求逆,主要时间花费在这里)
4.把△X拆分成各个顶点的值
5.调用顶点的oplusImpl函数,更新顶点的_estimate变量
6.回到第一步
template <int D, typename T>
class BaseVertex
模板参数D表示顶点的最小维度(即不是顶点状态变量的维度,而是流形空间最小表示维度),例如对于三维空间的旋转有三个自由度D=3;
模板参数T表示顶点的内部优化数据类型,例如对于3D旋转,T可以是四元数。
g2o本身已经定义了一些常用的顶点类型:
VertexSE2: public BaseVertex<3, SE2> // 2D pose Vertex, (x,y,theta)
VertexSE3: public BaseVertex<6, Isometry3> // Isometry3使欧式变换矩阵T,实质是4*4矩阵//6d vector (x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion)
VertexPointXY: public BaseVertex<2, Vector2>
VertexPointXYZ: public BaseVertex<3, Vector3>
VertexSBAPointXYZ: public BaseVertex<3, Vector3>// 地图点坐标(SBA:sparse bundle adjustment)
VertexSE3Expmap: public BaseVertex<6, SE3Quat>// SE(3)位姿
VertexCam: public BaseVertex<6, SBACam>// Camera pose vertex
VertexSim3Expmap: public BaseVertex<7, Sim3>// Sim(3)位姿
如果自定义继承需要覆盖。
setToRiginImpl()
--->顶点重置函数,设定被优化变量_estimate的原始值
oplusImpl(const double * update_)
--->顶点更新函数,用于更新H△x = b求解出的增量△x
--->update_是指向更新值的指针,使用前需要转换成真实的结构类型。不一定是顶点类型。比如update_可以是李代数,但顶点类型是李群。
read()/write()
--->负责读和写顶点,一般实现可以为空
setFixed(true):设置顶点不参与优化
setMarginalized(true)设置边缘化:https://zhuanlan.zhihu.com/p/37843131
--->G2O中对路标点设置边缘化(pPoint->setMarginalized(true))是为了在计算求解过程中,先消去路标点变量,实现先求解相机位姿,然后再利用求解出来的相机位姿反过来计算路标点的过程,目的是为了加速求解,并非真的将路标点给边缘化掉;而VINS中则真正需要边缘化掉滑动窗口中的最老帧或者次新帧,目的是希望不再计算这一帧的位姿或者与其相关的路标点,但是希望保留该帧对窗口内其他帧的约束关系。
可以使用esitimate()函数得到顶点的值。
连接一个顶点的边叫做一元边(Unary Edge),连接两个顶点的边叫做二元边(Binary Edge),连接多个顶点的边叫做多元边(Hyper Edge)。
template <int D, typename E, typename VertexXi>
class BaseUnaryEdge
一元边(Unary Edge):D表示测量值的维度,E表示测量值的类型,VertexXi表示顶点的类型。
template <int D, typename E, typename VertexXi, typename VertexXj>
class BaseBinaryEdge
二元边(Binary Edge):D表示测量值的维度,E表示测量值的类型,VertexXi和VertexXj表示二元边所连接的两个顶点的类型。
EdgeSE3Expmap: public BaseBinaryEdge<6, SE3Quat, VertexSE3Expmap, VertexSE3Expmap>// 6D edge between two Vertex6D
EdgeSE3ProjectXYZ: public BaseBinaryEdge<2, Vector2, VertexPointXYZ, VertexSE3Expmap>// BA中的重投影误差(3D-2D(u,v)误差),将地图点投影到相机坐标系下的相机平面。
EdgeProjectXYZ2UV: public BaseBinaryEdge<2, Vector2, VertexPointXYZ, VertexSE3Expmap>// 和上面差不多,表示重投影误差的边:https://blog.csdn.net/leaveforwaiting/article/details/89337318
EdgeSBACam: public BaseBinaryEdge<6, SE3Quat, VertexCam, VertexCam>// 6D edge between two VertexCam
EdgeSim3: public BaseBinaryEdge<7, Sim3, VertexSim3Expmap, VertexSim3Expmap>: // Sim3之间的相对误差,优化变量只有Sim3表示的pose
EdgeSim3ProjectXYZ: public BaseBinaryEdge<2, Vector2, VertexPointXYZ, VertexSim3Expmap>: // 重投影误差,优化变量Sim3位姿与地图点
具体用法可以参考:
g2o:VertexSE3Expmap、VertexSBAPointXYZ、EdgeProjectXYZ2UV头文件代码阅读_正一番薯的博客-CSDN博客_vertexsbapointxyz如果自定义继承需要覆盖。
computeError()
--->函数里面需要计算_error的值,其他顶点和测量值的成员变量参考其他例子。
--->如果计算误差时,观测值在减号前面,求导时需要加“-”。
linearizeOplus()
--->单顶点的计算_jacobianOplusXi矩阵,双顶点的还要计算_jacobianOplusXj矩阵。
--->_jacobianOplusXi = d(error)/d(vi), _jacobianOplusXj = d(error)/d(vj)
--->矩阵维度 = 观测值维度 * 顶点维度
initialEstimate()
--->根据一个顶点和一条边(测量),初始化(推算)另一个顶点的估计。一般可以不实现
_measurement; // 存储观测值
_error; // 存储computeError() 函数计算的误差
_vertices[]; // 存储顶点信息,比如二元边,_vertices大小为2,存储顺序和调用setVertex(int, vertex)和设定的int有关(0或1)
setId(int):定义边的编号(决定了在H矩阵中的位置)
setMeasurement():设置测量值
setVertex(int, vertex):设置边所连接的顶点
setLevel(int):设置边的level,默认是0
setInformation():设置信息矩阵
setRobustKernel():设置核函数
--->g2o::RobustKernelHuber* rk = new g2o::RobustKernelHuber;
--->edge->setRobustKernel(rk);
--->rk->setDelta(0.1);
David LEE:非线性优化(三):g2o源代码
参考:
深入理解图优化与g2o:g2o篇 - 半闲居士 - 博客园summer-ning:g2o李阳:非线性优化库之g2oSLAM本质剖析-G2O - 古月居






