- 手机:
- 18888889999
- 电话:
- 0898-66889888
- 邮箱:
- admin@youweb.com
- 地址:
- 海南省海口市玉沙路58号
图片、视频、时间序列等数据在计算机内都可以转换成不同维度的张量,神经网络就是通过对这些张量进行线性运算后再经过激活函数的非线性运算得到最终目的的过程,神经网络模型中有一些权重参数,这些参数对张量的运算过程有很大的影响,我们需要利用损失函数对这些参数进行求导,从而找出梯度下降的正确方向并往该方向更新参数,更新参数的方法即为优化器。
关键概念:
激活函数
损失函数
优化器
激活函数是神经网络中对输入数据进行计算的非线性函数,如果没有激活函数的加持,那么神经网络仅仅对输入数据做简单的线性变化,只能解决线性问题,如下图的二分类问题:

单层感知机就是一种单层的无激活函数的神经网络,它不能解决异或问题。(https://www.jianshu.com/p/853ebc9e69f6)
当有了激活函数的帮助,神经网络就可以解决很多的非线性问题,上面的二分类问题就可以用一条曲线分割开来,类似下图示例

1.1 常见的几种激活函数
1.1.1 Sigmoid
Sigmoid激活函数的形式为:
f
(
z
)
=
1
1
+
e
x
p
(
?
z
)
f(z)=\frac{1}{1+exp(-z)}
f(z)=1+exp(?z)1?
其几何图像如下:

特点:
它能够把输入的连续实值变换为0和1之间的输出,特别的,如果是非常大的负数,那么输出就是0;如果是非常大的正数,输出就是1.
缺点:在深度神经网络中梯度反向传递时导致梯度爆炸和梯度消失,其中梯度爆炸发生的概率非常小,而梯度消失发生的概率比较大。
Sigmoid激活函数的导函数为:
f
′
(
z
)
=
f
(
z
)
(
1
?
f
(
z
)
)
f'(z)=f(z)(1-f(z))
f′(z)=f(z)(1?f(z))
由导函数可见当f(z)趋向于0或1时,导函数趋向于0,从而导致梯度消失,从Sigmoid的函数图像中可以看出这时z趋向于无穷小或无穷大。
1.1.2 Tanh
Tanh激活函数的形式为:
f
(
z
)
=
e
z
?
e
?
z
e
z
+
e
?
z
f(z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{*z}}
f(z)=ez+e?zez?e?z?
其函数图像如下:

Tanh也会产生梯度消失问题,当z趋向于无穷大或者无穷小时都会产生梯度消失,实际上,Tanh激活函数相当于时Sigmoid的平移:
t
a
n
h
(
z
)
=
2
s
i
g
m
o
i
d
(
2
z
)
?
1
tanh(z)=2sigmoid(2z)-1
tanh(z)=2sigmoid(2z)?1
1.1.3 ReLu
ReLu激活函数形式如下:
f
(
z
)
=
m
a
x
(
0
,
z
)
f(z)=max(0,z)
f(z)=max(0,z)
其函数图像为:

ReLu激活函数相对于Sigmoid与Tanh的优点有:
(1)从计算的角度上,Sigmoid和Tanh激活函数均需要计算指数,复杂度高,而ReLU只需要一个阈值即可得到激活值。
(2)ReLU的非饱和性可以有效地解决梯度消失的问题,提供相对宽的激活边界。
(3)ReLU的单侧抑制提供了网络的稀疏表达能力。
更多激活函数相关请参考https://blog.csdn.net/tyhj_sf/article/details/79932893
计算预测值与真实值之间差距的函数,损失函数中的参数就是神经网络模型中所用的参数,通过损失函数对参数求导后导数的正负号来判断参数更新的变化方向,若导数为正数,参数减小的方向会使损失函数减小;若导数为负数,参数增大的方向会使损失函数较小。
2.1 常见的损失函数及其特点
2.1.1 二分类问题
对于二分类问题,样本标签Y={1,-1},一般用0-1损失函数,0-1损失函数为:

该损失函数能够直观地刻画分类的错误率,但是由于其非凸、非光滑的特点,使得算法很难直接对该函数进行优化。
0-1损失的一个代理损失函数是Hinge损失函数:
 Hinge损失函数是0-1损失函数相对紧的凸上界,且当fy≥1时,该函数不对其做任何惩罚。Hinge损失在fy=1处不可导,因此不能用梯度下降法进行优化,而是用次梯度下降法(Subgradient Descent Method)。0-1损失的另一个代理损失函数是Logistic损失函数:
Hinge损失函数是0-1损失函数相对紧的凸上界,且当fy≥1时,该函数不对其做任何惩罚。Hinge损失在fy=1处不可导,因此不能用梯度下降法进行优化,而是用次梯度下降法(Subgradient Descent Method)。0-1损失的另一个代理损失函数是Logistic损失函数:

当预测值在[-1,1]时,另一个常用的代理损失函数是交叉熵(Cross Entropy)损失函数:

交叉熵损失函数也是0-1损失函数的光滑凸上界。这四种损失函数的曲线如下图所示:

2.1.2 回归问题
对于回归问题,常用的是平方损失函数:

平方损失函数是光滑函数,能够用梯度下降法进行优化。然而,当预测值距离真实值越远时,平方损失函数的惩罚力度越大,因此它对异常点比较敏感。为了解决该问题,可以采用绝对损失函数:
 绝对损失函数相当于是在做中值回归,相比做均值回归的平方损失函数,绝对损失函数对异常点更鲁棒一些。但是,绝对损失函数在f=y处无法求导数。综合考虑可导性和对异常点的鲁棒性,可以采用Huber损失函数:
绝对损失函数相当于是在做中值回归,相比做均值回归的平方损失函数,绝对损失函数对异常点更鲁棒一些。但是,绝对损失函数在f=y处无法求导数。综合考虑可导性和对异常点的鲁棒性,可以采用Huber损失函数:
L
H
u
b
e
r
=
{
(
f
?
y
)
2
∣
f
?
y
∣
?
δ
2
δ
∣
f
?
y
∣
?
δ
2
∣
f
?
y
∣
>
δ
L_{Huber}=\left\{\begin{matrix} (f-y)^{2} & |f-y|\leqslant \delta \\ 2\delta |f-y|-\delta ^{2}&|f-y|>\delta \end{matrix}\right.
LHuber?={(f?y)22δ∣f?y∣?δ2?∣f?y∣?δ∣f?y∣>δ?
Huber损失函数在|f?y|较小时为平方损失,在|f?y|较大时为线性损失,处处可导,且对异常点鲁棒。这三种损失函数的曲线如下图

优化器是指更新神经网络模型参数所使用的算法。
3.1常用的优化器
3.1.1批量梯度下降(Batch gradient descent,BDG)
批量梯度下降法,也是梯度下降法最基础的形式,算法的思想是在更新每个参数的时,都使用所有样本进行更新。
批量梯度下降每迭代一步,是需要用到训练集的所有数据,如果样本数目很大,速度就会很慢,所有随机梯度下降(SGD)也就顺理成章的引入。
所以关于BGD的优缺点总结如下:
优点:全局最优解;易于并行实现;从跌代次数上来说,BGD的迭代次数比较少。
缺点:当样本数目很多时,训练过程会很慢
3.1.2随机梯度下降法(Stochastic Gradient Descent,SGD)
SGD及其变种是深度学习中应用最多的优化算法,随机梯度下降法本质上是采用迭代方式更新参数,每次迭代在当前位置的基础上,沿着某一方向迈一小步抵达下一位置,然后在下一位置重复上述步骤。随机梯度下降法用单个训练样本的损失来近似平均损失。因此,随机梯度下降法用单个训练数据即可对模型参数进行一次更新,大大加快了收敛速率。该方法也非常适用于数据源源不断到来的在线更新场景。
但是,SGD伴随的一个问题是噪音较多,使得SGD并不是每次迭代都向着整体最优化方向。
优点:训练速度快;
缺点:准确度下降,并不是全局最优;不易于并行实现。从迭代次数来看,SGD迭代次数较多,在解空间的搜索过程看起来很盲目。
3.1.3 小批量梯度下降(Mini-Batch Gradient Descent ,MBGD)
批量梯度下降法,也是梯度下降法最基础的形式,算法的思想是在更新每个参数的时,都使用所有样本进行更新。其训练速度较快。
优点:收敛更稳定,另一方面可以充分地利用深度学习库中高度优化的矩阵操作来进行更有效的梯度计算。
缺点:关于学习率的选择,如果太小,收敛速度就会变慢,如果太大,损失函数就会在极小值处不停的震荡甚至偏离。
3.1.4.动量算法(Momentum)
尽管随机梯度下降算法及其相关类型算法是当前很流行的优化算法,但是其学习过程有时会很慢。动量算法的出现解决了这一问题,它模拟的是物体运动时的惯性,即更新的时候在一定程度上保留之前更新的方向,同时利用当前batch的梯度微调最终的更新方向。其效果如下图:

上图红色路径是动量算法的路径,黑色箭头为随机梯度下降算法的路径。其数学表达大致如下:

3.1.5 Nesterov 动量
Nesterov 动量与标准动量之间的区别在于梯度计算上,Nesterov 动量中,梯度计算在当前速度之后,因此,Nesterov 动量可以解释为往标准动量中加入了一个校正因子。
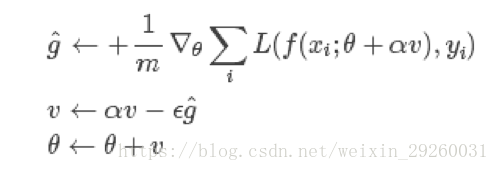
更多优化器相关信息可参考:
https://blog.csdn.net/weixin_29260031/article/details/82320525
https://blog.csdn.net/weixin_40170902/article/details/80092628?utm_medium=distribute.pc_relevant.none-task-blog-baidujs-2
(以上信息都是我参考相关书籍和博客总结整理的,如有错误之处,还望各位朋友纠正。)







