? ? ? ? 不管是初学者还是精通智能优化算法(粒子群算法，遗传算法等)的朋友，相信你们都对智能优化算法运行之慢深有体会，对于比较复杂的问题，经常出现运行一次几小时，调试一次几小时的情况。调试了这么多年代码，智能优化算法对我来说算是老朋友了，平时也积累了一些提高智能优化算法运行效率的办法，在此分享给大家。

这篇博客以粒子群算法为例，说明使用matlab编程时，如何减少粒子群算法运行时间。要解决的目标函数为：

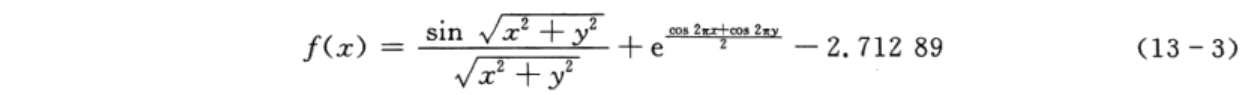其中，变量x和y都属于[-10,10]的区间，要求出f(x)的最大值。

matlab绘图代码和图像如下：

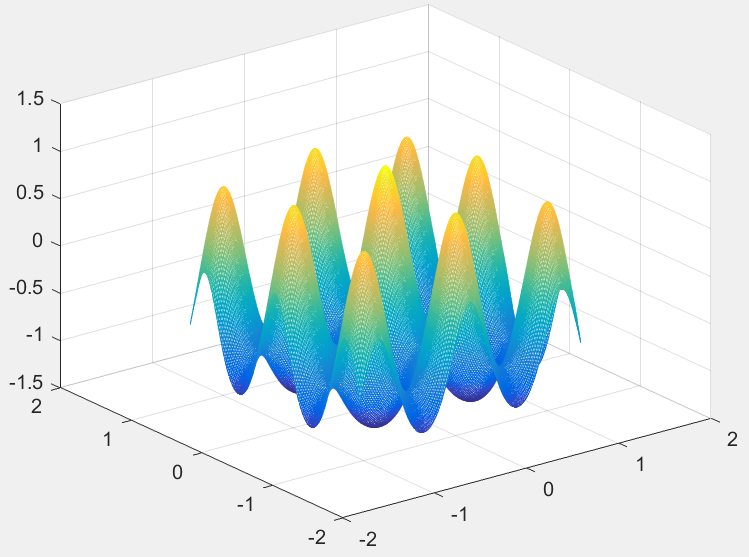
从函数图形可以看出，该函数有很多局部极大值点，而极值位置为(0,0)，在(0,0)附近取得极大值。

粒子群算法(particle swarm optimization,PSO)最早由Kennedy和Eberhart在1995年提出的，源于对鸟类捕食行为的研究，算法中每个粒子都代表问题的一个潜在解，每个粒子对应一个由适应度函数决定的适应度值。粒子的速度决定了粒子移动的方向和距离，速度随自身及其他粒子的移动经验进行动态调整，从而实现个体在可解空间中的寻优。

PSO算法首先在可行解空间中初始化一群粒子，每个粒子都代表极值优化问题的一个潜在最优解，用位置、速度和适应度值三项指标表示该粒子特征，适应度值由适应度函数计算得到，其值的好坏表示粒子的优劣。粒子在解空间中运动，通过跟踪个体极值Pbest和群体极值Gbest更新个体位置。个体极值Pbest是指个体所经历位置中计算得到的适应度值最优位置，群体极值Gbest是指种群中的所有粒子搜索到的适应度最优位置。粒子每更新一次位置，就计算一次适应度值，并且通过比较新粒子的适应度值和个体极值、群体极值的适应度值更新个体极值Pbest和群体极值Gbest位置。

实现粒子群算法求解上述优化问题的原始代码如下：

当种群规模为500，最大迭代次数为500时，粒子群算法某次运行结果如下：

我们可以看到，大约1秒的时间，粒子群算法可以求出最优解为[-1.4828e-9,-5.222e-10]，非常接近最优解[0,0]。

其实这份代码在运行时间上还有很大的改进空间，我们可以分块来看。%% 清除变量、%% 设置种群参数与%% 种群初始化这几步基本上都是最优的写法。主要是求适应度和迭代求最优解这里存在循环语句，可以改进写法。

首先来看%% 初始的适应度这块代码：

这里用到的循环语句，运行时间肯定会偏长。那么我们可不可以改写这部分代码，去掉循环语句，同时保持效果不变？当然是可以的，但首先需要改写一下fun函数，初始的fun函数是这样的：

由于我们最开始默认传入fun函数的变量pop只代表一个粒子，所以是一个1×2的变量，就可以令x = pop(1)，令y = pop(2)，计算得到的输出变量fitness也是一个1×1的标量。如果输入变量pop是一个n×2的变量，就不能这样写了，需要把fun函数改写成：

这样就可以输入一个n×2的变量pop，输出一个n×1变量fitness，直接计算所有粒子的适应度。同时在主函数部分也需要把代码修改为：

同时也省去了前面初始化的一些代码。

再来看迭代求最优解的部分。首先这里也包括了求适应度的部分，可以直接沿用上面的成果。对于速度和位置的更新，还有进一步改进的空间。

这部分速度慢的原因同样也是因为有一个for循环，使用matlab中向量化的运算可以避免使用for循环，同时保持代码的效果不变，具体如下：

? ? ? ? 1)速度的更新。在更新速度时，可以采用矢量化的方式。由于对每个粒子都需要生成随机数r1和r2，所以r1和r2的维度应该都是sizepop×1，另外为了可以使用.*运算使r1和pop_v每个元素可以对应相乘，还将其乘上一个全为1的1×dim向量ones(1,dim)。

而对越限速度的处理方式用到了matlab矩阵中的逻辑索引方式，这里不再赘述，具体可以参考官方文档(查找符合条件的数组元素 - MATLAB & Simulink - MathWorks 中国)

? ? ? ? 2)位置的更新，位置的更新直接使用矩阵加法，对位置越限粒子的处理和速度越限时的处理一致。

? ? ? ? 3)更新群体所有的适应度的方法和上面提到的一样，而更新群体最优和个体最优时则需要使用到if语句和逻辑索引。

经过我们的处理，除了迭代求最优解，其他所有的循环语句都被消除了，修改后完整的代码如下：

运行结果：

? ? ? ? ?求出的最优解也很接近实际最优解[0,0]，同时求解时间从接近1秒大幅减小到0.06秒，减小的比例达到了惊人的94%！！

当然，由于粒子群算法是一个随机搜索，时间也具有偶然性，我们多试几次，求平均值，结果如表1所示：?

表1 优化前和优化后代码运行时间对比

次数	优化前/秒	优化后/秒
1	0.97273	0.06014
2	0.94861	0.058207
3	1.0526	0.056668
4	0.97083	0.056835
5	1.0751	0.058857
6	0.9547	0.055463
7	0.98452	0.060969
8	1.1933	0.057191
9	0.98235	0.060772
10	1.0497	0.05734
平均值	1.018444	0.0582442

即使是平均值，也相差了94.28%，和我们之前对比的结果相差不大。

? ? ? ? 这是一个二维小规模的优化问题，从时间的减少上可能看不出很大的效果，但如果问题的规模很大，算法运行时动不动就要好几个小时，即使能提升50%的运行效率，也能大大节省我们的时间。