本期为大家介绍骑手优化算法(Rider Optimization Algorithm,ROA)。该算法由D. Binu等人于2018年提出，主要模拟了在比赛中骑手通过身份划分来引导整个团队走向胜利的过程。因其在模拟电路的故障诊断中具有较好的效果，故在近年来引起了一定的关注。

顾名思义，ROA算法考虑了一个骑手群体，他们相互协作以使团队获得胜利。其中算法将一个团队均分为四个小组，分别记为绕行手、跟随手、超车手和冲刺手(原文中叫做攻击者，但我认为在这里叫做冲刺手更好)。

尽管车手遵循预先确定的策略，但达到目标的主要因素是通过正确操纵方向盘、齿轮、加速器和制动器。对于每一个时刻，骑手都会通过调整这些参数来改变他们朝向目标的位置，并遵循基于当前成功率的预定义策略，所以该算法涉及了很多参数。

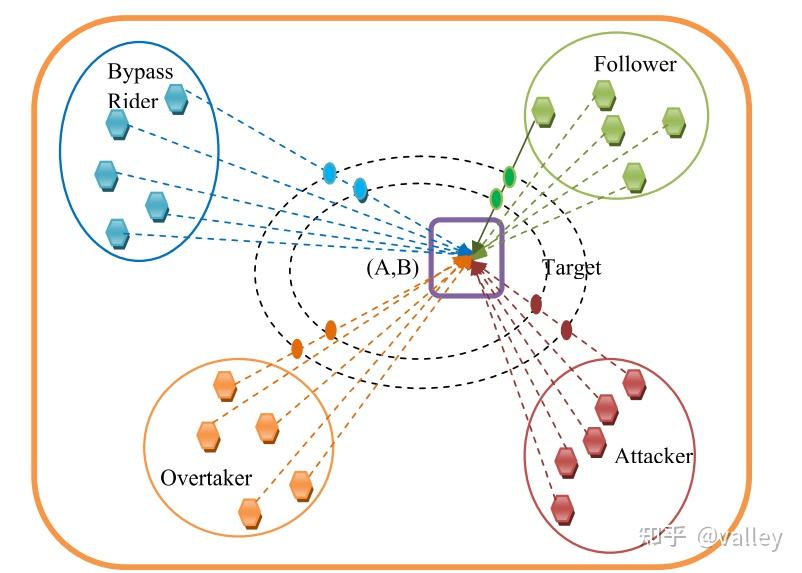
首先我们对四种骑手进行介绍：

(a).绕行手：绕行手通过绕行引导路径到达目标。这意味着其不跟随领先骑手(种群最优个体)。

(b).跟随手：跟随手在大部分区域内依赖或跟随领先骑手。

(c).超车手：这类骑手根据自身当前位置及领先骑手的位置来调整下一步行动。

(d).冲刺手：其根据其他骑手的位置以最大速度到达目标点。

种群位置初始化

首先将种群G均分为四组：绕行手(B)、跟随手(F)、超车手(O)、冲刺手(A)：

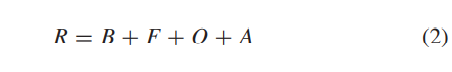
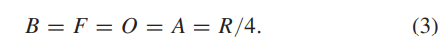
其中R为种群规模，接下来就是熟悉的随机初始化。

参数初始化

前文提到，种群中的各种参数对算法起了重要的引导作用。首先是骑手的转向角T：

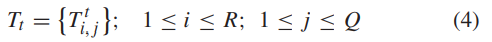
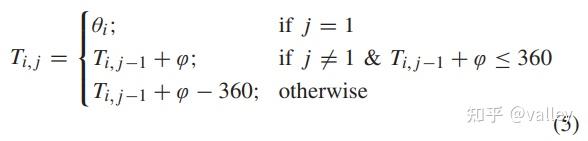
其中Q为空间维度，位置角 和坐标角 的计算方式为：

注意，只有初始化阶段才采取这种更新方式，在迭代中是另一种方式。

下面说一下齿轮E：

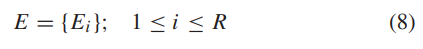
初始时所有个体的齿轮参数均设为，迭代时其值从{0,1,2,3,4}中选取，具体选择方式我们下文再介绍。

接下来是加速度e 和制动器K：

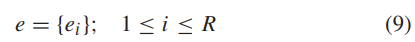
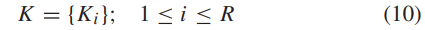
把它们放在一起的原因就是其值均处于[0,1]内，但前者初始为0，后者为1。

速度限制

不同于粒子群将粒子速度限制在特定范围内，该算法选择了一种动态速度边界：

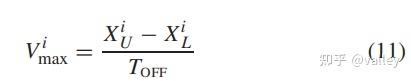
其中XU、XL分别为骑手i 在此次迭代时的位置上、下限，TOFF即为停止时间，对应最大迭代次数。因此，骑手i 的齿轮对速度的限制为;

这里|E|为齿轮数，算法中取5。

寻找成功率

成功率是根据骑手位置和目标位置之间的距离计算得出的：

这里Xi 为当前骑手i 的位置，LT为目标位置。注意，这是理论上的成功率，在算法中，成功率就是适应度值！！！

绕行手位置更新

绕行手绕过公共路径，因此位置更新是随机的：

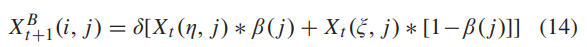
其中 、 (j )均为[0,1]内一随机数， 、 均为[1,R]内一随机整数，表示随机选择出的一个骑手。通俗的来讲，绕行手就不合群，非要自己单干。

跟随手位置更新

跟随手通过跟随领先者来更新他的位置：

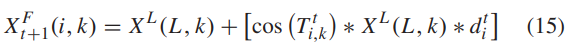
式中k 为当前空间维度，XL为领导者L的位置，d 的计算方式为：

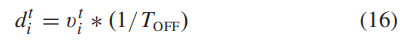
可以看出，能不能跟上领导，还得看自身的速度呀。注意，这个速度就和我们之前提到的各种参数有关了：

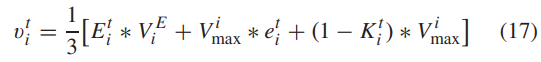
注意注意！并不是每个跟随手的每个维度都要更新！是否更新取决于坐标选择器PON：

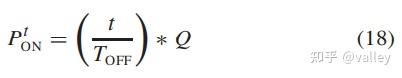
这里t 为当前迭代次数，TOFF大家就默认它是最大迭代次数吧。将其与相应的维度指数相乘，并将结果与空间维度Q进行比较，以确定位置变化需要考虑的坐标：

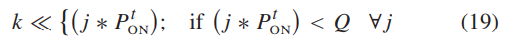
所以，有些领导不是我们想跟就能跟得上哈哈。

超车手位置更新

超车手的位置更新相对来说也有点复杂：

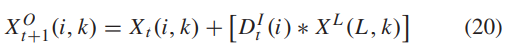
式中的k 为当前维度，D为当前个体的方向指示器，毕竟没有一个合适的方向，怎么超车嘛：

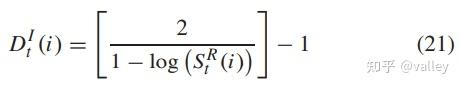
其中SR 为相对成功率，超车手的相对成功率由其适应度值与种群内最差个体的适应度值之比确定：

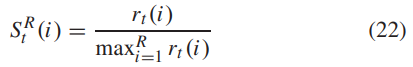
同跟踪手，为了确定要更新的维度，首先要确定当前超车手与最优个体的间距：

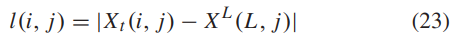
之后要通过对比当前超车手各维度的平均位置 来确定：

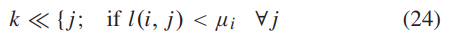
冲刺手的位置更新

试图超越领导者的冲刺手遵循与跟随手类似的更新过程。但是，冲刺手会更新坐标中的所有值，而不仅仅是选定维度中的值：

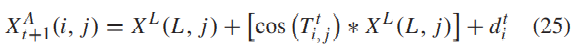
这里各参数与前文相同。

参数更新

各参数的更新主要与活动计数器A有关：

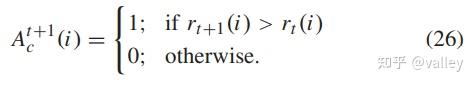
好了，下面一一介绍。转向角的更新方式为：

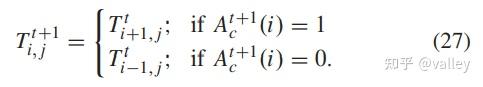
齿轮的更新方式为：

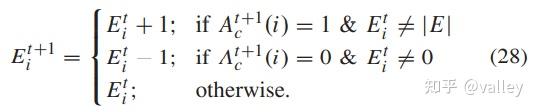
加速度的更新方式为：

制动器的更新方式为：

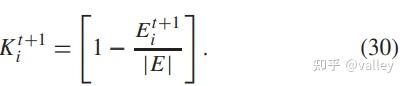
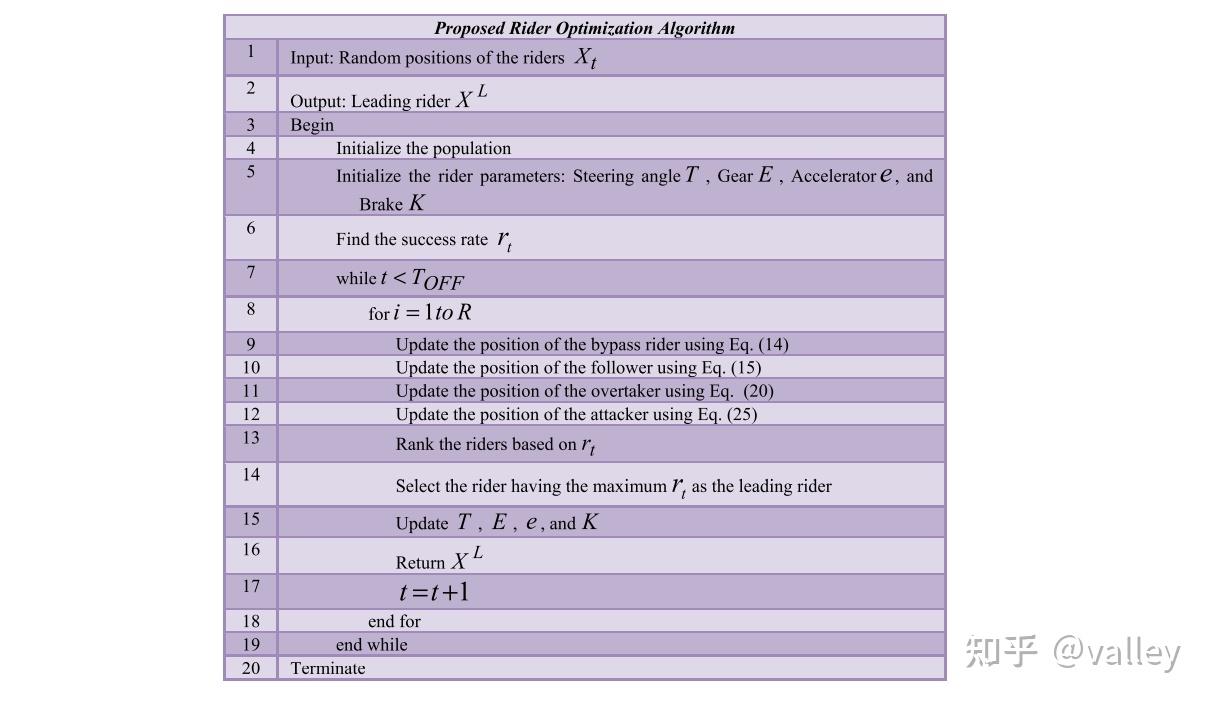
至此，算法迭代伪代码为：

本期我们将ROA算法与往期的冠状病毒群体免疫优化器(CHIO)、政治优化器(PO)在部分CEC2017测试函数上进行对比测试，取种群规模为100，维度为100，最大迭代次数为10000，计算结果如下：

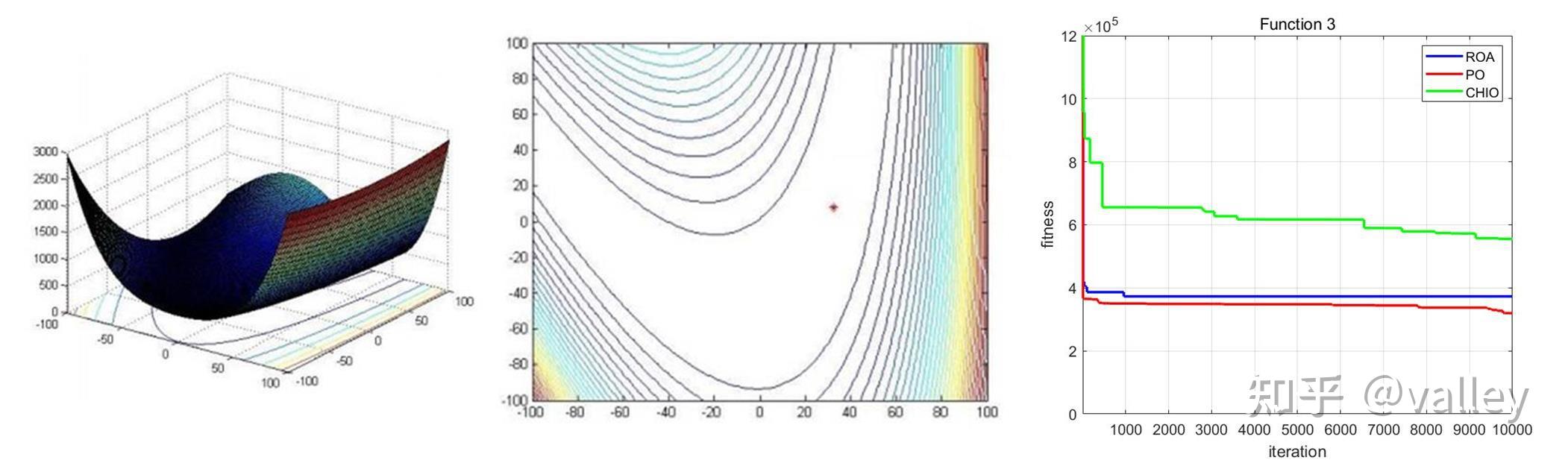
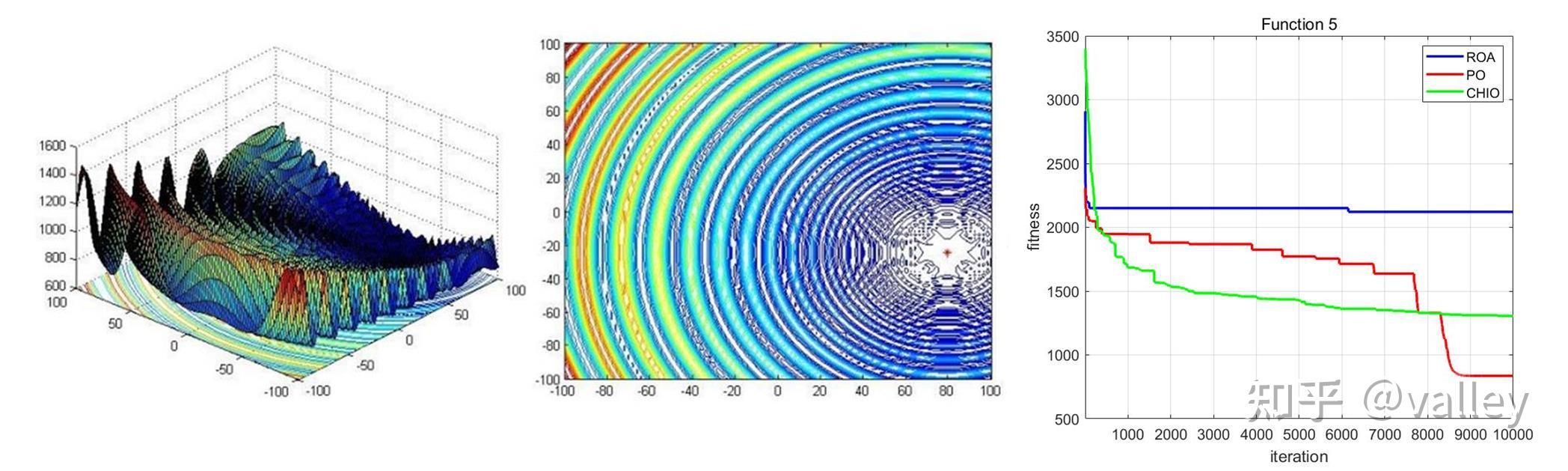
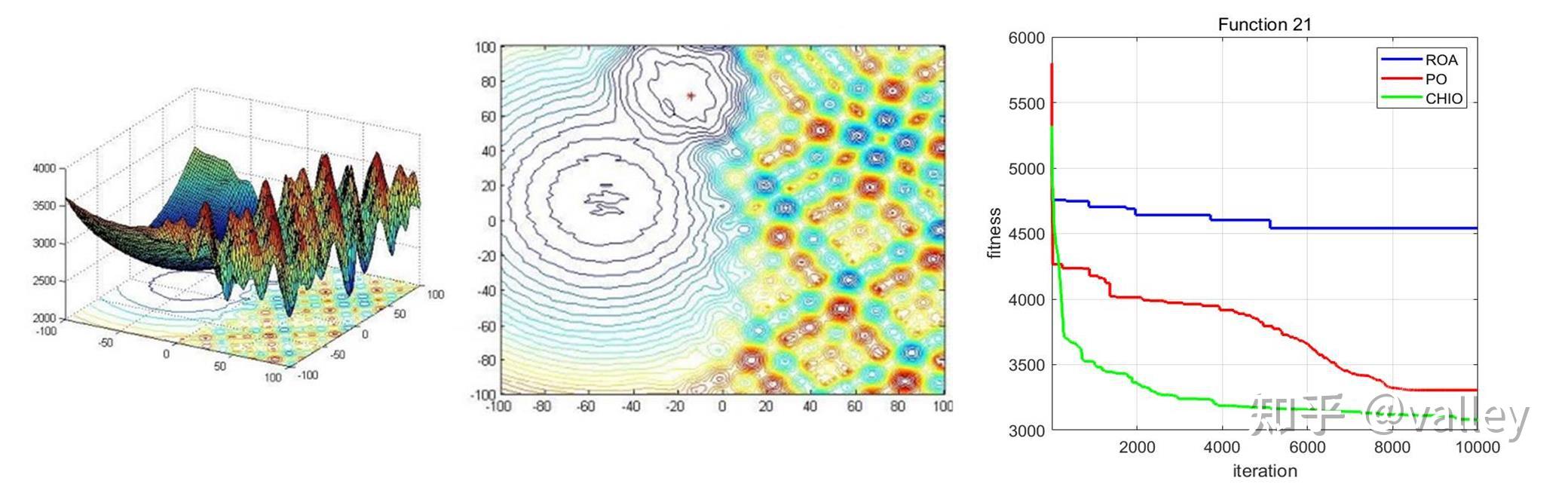
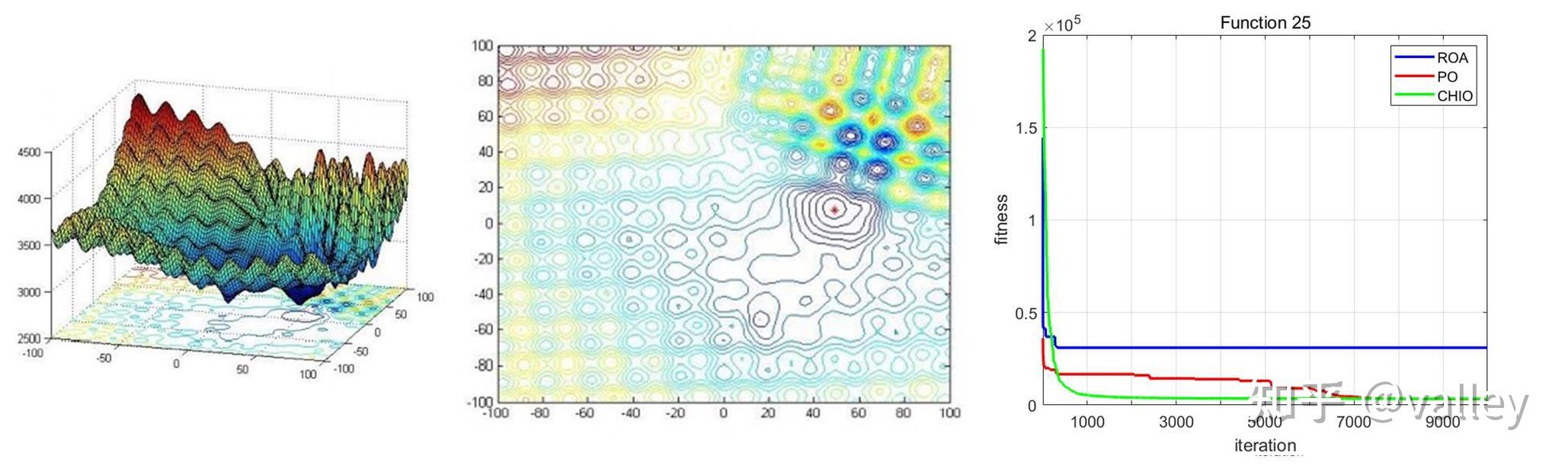
就迭代曲线来看，对于较简单的多峰函数ROA算法还能应对一下，随着函数复杂度的增加就开始吃力了。总体上感觉跳出局部最优值的能力有待提升。

总体来说，ROA算法结构非常复杂，主要涉及了四种个体的迭代行为，其中的关键是各类自适应参数。可以看出，冲刺手相对于其他骑手可以较快的靠近最优骑手，而且超车手能够对全局进行充分的探索以获得更快的收敛速度。但是算法复杂度过高，而且我认为在式(25)中过多体现了最优个体的位置引导作用，自身速度影响其实比较小。毕竟冲刺手的作用是追赶甚至超越最优骑手，所以他的速度还是蛮重要的。如果这里对两者分别添加比例系数，说不定能更好些~