欧陆资讯 NEWS CENTER
联系我们 CONTACT US
- 手机:
- 18888889999
- 电话:
- 0898-66889888
- 邮箱:
- admin@youweb.com
- 地址:
- 海南省海口市玉沙路58号
常见路径规划算法代码-Matlab (纯代码篇)
2024-07-08 21:35:16 点击量:
此文并没有太多的食用价值,只是将下面这篇文章中人工势场法、A*算法、DWA(动态窗口法)、RRT star 算法这四个算法的代码复制粘贴到此文中。既方便大伙打开文章就能看代码,也能解决因为matlab版本差异导致的中文注释乱码的问题。
下面这篇文章是对这几个算法的简单演示与介绍。Poao:常见路径规划算法实现-Matlab
此文代码下载: Poao-路径规划算法.zip - 蓝奏云
哈哈哈,终于找到机会水一篇文章咯。
重点:务必要借助目录进行跳转,不然会发疯的!!
目录中的二级小标题即为该算法下的子文件名,大伙们完全可以复制粘贴此文中的代码并创建对应的.m文件。
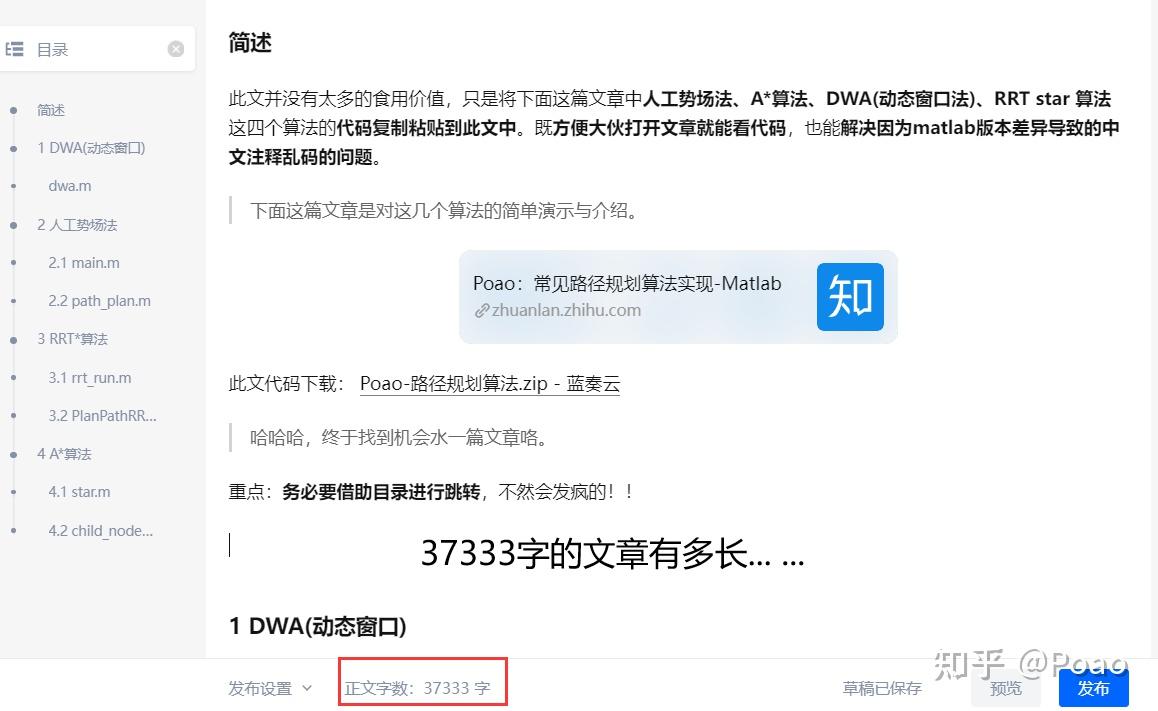
下图中,移动的小圆圈为机器人、蓝色的线束为预测的路径、紫色的椭圆为障碍物、红色的※标志着机器人的目标点。
DWA算法皆在“dwa.m”文件中,算法的实现流程在 DynamicWindowApproach 函数中,其具体功能实现则需主要关注Evaluation、GenerateTrajectory、CalcDynamicWindow等函数。
% -------------------------------------------------------------------------
% File : DWA 算法
% Discription : Mobile Robot Motion Planning with Dynamic Window Approach
% Author :Yuncheng Jiang
% License : Modified BSD Software License Agreement
% 出处:https://b23.tv/rGKUTW - b站up主【WHEELTEC】
% 源代码已经配备丰富的注释,我在其基础上添加了一些个人理解。
% —— 2021/10/30 Poaoz
% -------------------------------------------------------------------------
% 流程梳理 - dwa动态窗口算法
% 1)设置初始化参数:起点、终点、障碍物、小车的速度加速度限制等
% 2)根据小车当前状态及参数,计算出小车接下来一小段时间可达到的状态(主要为速度、加速度范围)
% 3)根据上述计算而得的速度、加速度,模拟出小车接下来一小段时间可达到的路径
% 4) 借助评价函数,对上述路径进行评估,并选取出最优解,然后使小车执行(执行对应的速度、角速度)
% 5)再以小车新的位置及状态为基础,重复上述“2-5”,直到判断出小车到达终点。
% 闲谈:前面学习了RRT、A*、人工势能法,综合来看,这几种方法的套路是类似的。
% 相比较,DWA更加灵活,无需栅格化地图并且更贴合小车运动实际。
% 该函数相当于dwa算法的main函数,内容包括 参数设定、流程的梳理、绘图 。
function []= dwa_V_1_0()
close all;
clear ;
disp('Dynamic Window Approach sample program start!!')
%% 机器人的初期状态[x(m),y(m),yaw(Rad),v(m/s),w(rad/s)]
% x=[0 0 pi/2 0 0]'; % 5x1矩阵 列矩阵 位置 0,0 航向 pi/2 ,速度、角速度均为0
x = [0 0 pi/10 0 0]';
% 下标宏定义 状态[x(m),y(m),yaw(Rad),v(m/s),w(rad/s)]
POSE_X = 1; %坐标 X
POSE_Y = 2; %坐标 Y
YAW_ANGLE = 3; %机器人航向角
V_SPD = 4; %机器人速度
W_ANGLE_SPD = 5; %机器人角速度
goal = [10,10]; % 目标点位置[x(m),y(m)]
% 障碍物位置列表[x(m) y(m)]
obstacle=[%0 2;
3 10*rand(1);
% 4 4;
% 5 4;
% 5 5;
6 10*rand(1);
% 5 9
% 7 8
8 10*rand(1);
2 5;
4 2;
7 7;
9 9
];
%边界障碍物,防止跑出图外
for i =-1
for j = -1:12
obstacle = [obstacle; [i,j]];
end
end
for i =12
for j = -1:12
obstacle = [obstacle; [i,j]];
end
end
for j =-2
for i = -1:12
obstacle = [obstacle; [i,j]];
end
end
for j=13
for i= -1:12
obstacle = [obstacle; [i,j]];
end
end
obstacleR = 0.5;% 冲突判定用的障碍物半径
global dt;
dt = 0.1;% 时间[s]每一条计算得到的路径,由多个点组成 dt即为每个点之间的时间间隔
% evalParam[4]/dt+1=每条路径的构成点数目 这两个参数更改后,dwa算法的具体效果也将有所变化
% 机器人运动学模型参数
% 最高速度m/s],最高旋转速度[rad/s],加速度[m/ss],旋转加速度[rad/ss],
% 速度分辨率[m/s],转速分辨率[rad/s]]
Kinematic = [1.0,toRadian(20.0),0.2,toRadian(50.0),0.01,toRadian(1)]; % 调用函数里面的 model
%定义Kinematic的下标含义 % Kinematic 在路径计算相关函数中,大量用到
MD_MAX_V = 1;% 最高速度m/s]
MD_MAX_W = 2;% 最高旋转速度[rad/s]
MD_ACC = 3;% 加速度[m/ss]
MD_VW = 4;% 旋转加速度[rad/ss]
MD_V_RESOLUTION = 5;% 速度分辨率[m/s]
MD_W_RESOLUTION = 6;% 转速分辨率[rad/s]]
% 评价函数参数[heading,dist,velocity,predictDT]
% 航向得分的比重、距离得分的比重、速度得分的比重、向前模拟轨迹的时间
evalParam = [0.045, 0.1 ,0.1, 3.0];
% evalParam=[2, 0.2 ,0.2, 3.0];
area = [-3 14 -3 14];% 模拟区域范围[xmin xmax ymin ymax]
% 模拟实验的结果
result.x=[]; %累积存储走过的轨迹点的状态值
tic; % 估算程序运行时间开始
flag_obstacle = [1-2*rand(1) 1-2*rand(1) 1-2*rand(1)];
vel_obstacle = 0.05;
temp = 0;
abc = 0;
%movcount=0;
%% Main loop 循环运行 5000次 指导达到目的地 或者 5000次运行结束
for i = 1:5000
% DWA参数输入 返回控制量 u=[v(m/s),w(rad/s)]和 轨迹 ~ 即机器人将采用的控制参数
[u,traj] = DynamicWindowApproach(x,Kinematic,goal,evalParam,obstacle,obstacleR); % 算出下发速度u/当前速度u
x = f(x,u); % 机器人移动到下一个时刻的状态量 根据当前速度和角速度推导 下一刻的位置和角度
abc = abc+1;
% 历史轨迹的保存
result.x = [result.x; x']; %最新结果 以行的形式 添加到result.x,保存的是所有状态参数值,包括坐标xy、朝向、线速度、角速度,其实应该是只取坐标就OK
% 是否到达目的地
if norm(x(POSE_X:POSE_Y)-goal')<0.25 % norm函数来求得坐标上的两个点之间的距离
disp('==========Arrive Goal!!==========');break;
end
%====Animation====
hold off; % 关闭图形保持功能。 新图出现时,取消原图的显示。
ArrowLength = 0.5; % 箭头长度
% 机器人 ~ 绘图操作
% quiver(x,y,u,v) 在 x 和 y 中每个对应元素对组所指定的坐标处将向量绘制为箭头
quiver(x(POSE_X), x(POSE_Y), ArrowLength*cos(x(YAW_ANGLE)), ArrowLength*sin(x(YAW_ANGLE)),'ok');
% 绘制机器人当前位置的航向箭头
hold on;
%启动图形保持功能,当前坐标轴和图形都将保持,从此绘制的图形都将添加在这个图形的基础上,并自动调整坐标轴的范围
plot(result.x(:,POSE_X),result.x(:,POSE_Y),'-b');hold on; % 绘制走过的所有位置 所有历史数据的 X、Y坐标
plot(goal(1),goal(2),'*r');hold on; % 绘制目标位置
for j = 1:3
if obstacle(j,2) > 10 && flag_obstacle(j) > 0 || obstacle(j,2) < 0 && flag_obstacle(j) < 0
flag_obstacle(j) = -flag_obstacle(j);
end
% obstacle(j,2)=obstacle(j,2)+flag_obstacle(j)*vel_obstacle;
end
%plot(obstacle(:,1),obstacle(:,2),'*k');hold on; % 绘制所有障碍物位置
DrawObstacle_plot(obstacle,obstacleR);
% 探索轨迹 画出待评价的轨迹
if ~isempty(traj) %轨迹非空
for it=1:length(traj(:,1))/5 %计算所有轨迹数 traj 每5行数据 表示一条轨迹点
ind = 1+(it-1)*5; %第 it 条轨迹对应在traj中的下标
plot(traj(ind,:),traj(ind+1,:),'-g');hold on; %根据一条轨迹的点串画出轨迹 traj(ind,:) 表示第ind条轨迹的所有x坐标值 traj(ind+1,:)表示第ind条轨迹的所有y坐标值
end
end
axis(area); %根据area设置当前图形的坐标范围,分别为x轴的最小、最大值,y轴的最小最大值
grid on;
drawnow limitrate; %刷新屏幕. 当代码执行时间长,需要反复执行plot时,Matlab程序不会马上把图像画到figure上,这时,要想实时看到图像的每一步变化情况,需要使用这个语句。
for j = 1:3
if norm(obstacle(j,:)-x(1:2)')-obstacleR < 0
disp('==========Hit an obstacle!!==========');
temp = 1;
break;
end
end
if temp == 1
break;
end
% movcount=movcount+1;
% mov(movcount)=getframe(gcf);% 记录动画帧
end
toc; %输出程序运行时间 形式:时间已过 ** 秒。
disp(abc)
%movie2avi(mov,'movie.avi'); %录制过程动画 保存为 movie.avi 文件
%% 绘制所有障碍物位置 ok
% 输入参数:obstacle 所有障碍物的坐标 obstacleR 障碍物的半径
function []= DrawObstacle_plot(obstacle,obstacleR)
r = obstacleR;
theta = 0:pi/20:2*pi;
for id=1:length(obstacle(:,1))
x = r * cos(theta) + obstacle(id,1);
y = r *sin(theta) + obstacle(id,2);
plot(x,y,'-m');
end
%plot(obstacle(:,1),obstacle(:,2),'*m');hold on; % 绘制所有障碍物位置
%% DWA算法实现 ok
% model 机器人运动学模型 最高速度[m/s],最高旋转速度[rad/s],加速度[m/ss],旋转加速度[rad/ss], 速度分辨率[m/s],转速分辨率[rad/s]]
% 输入参数:当前状态、模型参数、目标点、评价函数的参数、障碍物位置、障碍物半径
% 返回参数:控制量 u=[v(m/s),w(rad/s)]和 轨迹集合 N * 31 (N:可用的轨迹数)
% 选取最优参数的物理意义:在局部导航过程中,使得机器人避开障碍物,朝着目标以较快的速度行驶。
function [u,trajDB]= DynamicWindowApproach(x,model,goal,evalParam,ob,R)
% Dynamic Window[vmin,vmax,wmin,wmax]最小速度 最大速度 最小角速度 最大角速度速度
Vr = CalcDynamicWindow(x,model); % 1)根据当前状态 和 运动模型 计算当前的参数允许范围
% 评价函数的计算 evalDB N*5 每行一组可用参数 分别为 速度、角速度、航向得分、距离得分、速度得分
% trajDB 每5行一条轨迹 每条轨迹都有状态x点串组成
[evalDB,trajDB]= Evaluation(x,Vr,goal,ob,R,model,evalParam); % 2)evalParam 评价函数参数[heading,dist,velocity,predictDT]
if isempty(evalDB)
disp('no path to goal!!');
u=[0;0];return;
end
% 各评价函数正则化
evalDB = NormalizeEval(evalDB);
% 3)最终评价函数的计算 - 从诸多可以选择的轨迹中,选择一个“最优”的路径
feval=[];
for id=1:length(evalDB(:,1)) % 遍历各个可运行的路径,分别计算其评价得分
feval = [feval;evalParam(1:3)*evalDB(id,3:5)']; %根据评价函数参数 前三个参数分配的权重 计算每一组可用的路径参数信息的得分
end
evalDB = [evalDB feval]; % 最后一组;加最后一列,每一组速度的最终得分
[maxv,ind] = max(feval);% 4)选取评分最高的参数 对应分数返回给 maxv 对应下标返回给 ind
u = evalDB(ind,1:2)';% 返回最优参数的速度、角速度
%% 评价函数 内部负责产生可用轨迹 ok
% 输入参数 :当前状态、参数允许范围(窗口)、目标点、障碍物位置、障碍物半径、评价函数的参数
% Vr保存着机器人当前状态可达到的 最小最大的速度与角速度 model保存着机器人的一些性能参数,如该函数中使用的 速度和角速度的分辨率
% 返回参数: (返回一堆可以行进的轨迹~这些轨迹还需进行评价函数的筛选,从而得到最终的前进路径)
% evalDB N*5 每行一组可用参数 分别为 速度、角速度、航向得分、距离得分、速度得分
% trajDB 每5行一条轨迹 每条轨迹包含 前向预测时间/dt + 1=31 个轨迹点(见生成轨迹函数)
function [evalDB,trajDB]= Evaluation(x,Vr,goal,ob,R,model,evalParam)
evalDB = [];
trajDB = [];
for vt = Vr(1):model(5):Vr(2) %根据速度分辨率遍历所有可用速度: 最小速度和最大速度 之间 速度分辨率 递增
for ot=Vr(3):model(6):Vr(4) %根据角度分辨率遍历所有可用角速度: 最小角速度和最大角速度 之间 角度分辨率 递增
% 轨迹推测; 得到 xt: 机器人向前运动后的预测位姿; traj: 当前时刻 到 预测时刻之间的轨迹(由轨迹点组成)
[xt,traj] = GenerateTrajectory(x,vt,ot,evalParam(4)); %evalParam(4),前向模拟时间;
% 各评价函数的计算
heading = CalcHeadingEval(xt,goal); % 前项预测终点的航向得分 偏差越小分数越高
[dist,Flag] = CalcDistEval(xt,ob,R); % 前项预测终点 距离最近障碍物的间隙得分 距离越远分数越高
vel = abs(vt); % 速度得分 速度越快分越高
stopDist = CalcBreakingDist(vel,model); % 制动距离的计算
if dist > stopDist && Flag == 0 % 如果可能撞到最近的障碍物 则舍弃此路径 (到最近障碍物的距离 大于 刹车距离 才取用)
evalDB = [evalDB;[vt ot heading dist vel]]; % flag 是否会碰到障碍物的标志
trajDB = [trajDB;traj]; % 每5行 一条轨迹
end
end
end
%% 归一化处理 ok
% 每一条轨迹的单项得分除以本项所有分数和
function EvalDB=NormalizeEval(EvalDB)
% 评价函数正则化
if sum(EvalDB(:,3))~= 0 % 航向得分
EvalDB(:,3) = EvalDB(:,3)/sum(EvalDB(:,3)); %矩阵的数除 单列矩阵的每元素分别除以本列所有数据的和
end
if sum(EvalDB(:,4))~= 0 % 距离得分
EvalDB(:,4) = EvalDB(:,4)/sum(EvalDB(:,4));
end
if sum(EvalDB(:,5))~= 0 % 速度得分
EvalDB(:,5) = EvalDB(:,5)/sum(EvalDB(:,5));
end
%% 单条轨迹生成、轨迹推演函数. ok
% 输入参数: 当前状态、vt当前速度、ot角速度、evaldt 前向模拟时间、机器人模型参数(没用到)
% 返回参数; 返回 预测的x和到达该x所经过的若干点 (将后者依次连线,就可得到一条预测的轨迹)
% x : 机器人模拟时间内向前运动 预测的终点位姿(状态);
% traj: 当前时刻 到 预测时刻之间 过程中的位姿记录(状态记录) 当前模拟的轨迹
% 轨迹点的个数为 evaldt / dt + 1=3.0 / 0.1 + 1=31
function [x,traj]= GenerateTrajectory(x,vt,ot,evaldt)
global dt;
time = 0;
u = [vt;ot];% 输入值
traj = x; % 机器人轨迹
while time <= evaldt
time = time+dt; % 时间更新
x = f(x,u); % 运动更新 前项模拟时间内 速度、角速度恒定
traj = [traj x]; % 每一列代表一个轨迹点 一列一列的添加
end
%% 计算制动距离 ok
%根据运动学模型计算制动距离, 也可以考虑成走一段段圆弧的累积 简化可以当一段段小直线的累积
% 利用 当前速度和机器人可达到的加速度,计算其速度减到0所走距离
function stopDist = CalcBreakingDist(vel,model)
global dt;
MD_ACC = 3;% 加速度
stopDist=0;
while vel>0 %给定加速度的条件下 速度减到0所走的距离
stopDist = stopDist + vel*dt;% 制动距离的计算
vel = vel - model(MD_ACC)*dt;%
end
%% 障碍物距离评价函数 ok
%(机器人在当前轨迹上与最近的障碍物之间的距离,如果没有障碍物则设定一个常数)
% 输入参数:位姿、所有障碍物位置、障碍物半径
% 输出参数:当前预测的轨迹终点的位姿距离所有障碍物中最近的障碍物的距离 如果大于设定的最大值则等于最大值
% 距离障碍物距离越近分数越低
function [dist,Flag]= CalcDistEval(x,ob,R)
dist=100; % 无障碍物的默认值
for io = 1:length(ob(:,1))
disttmp = norm(ob(io,:)-x(1:2)')-R; % 位置x到某个障碍物中心的距离 - 障碍物半径 !!!有可能出现负值吗
if disttmp <0 % 该位置会碰到障碍物
Flag = 1;
break;
else % 碰不到障碍物
Flag = 0;
end
if dist > disttmp % 大于最小值 则选择最小值
dist = disttmp;
end
end
% 障碍物距离评价限定一个最大值,如果不设定,一旦一条轨迹没有障碍物,将太占比重
if dist >= 3*R %最大分数限制
dist = 3*R;
end
%% heading的评价函数计算 ok
% 输入参数:当前位置、目标位置
% 输出参数:航向参数得分=180 - 偏差值
% 当前车的航向和相对于目标点的航向 偏离程度越小 分数越高 最大180分
function heading = CalcHeadingEval(x,goal)
theta = toDegree(x(3));% 机器人朝向
goalTheta = toDegree(atan2(goal(2)-x(2),goal(1)-x(1)));% 目标点相对于机器人本身的方位
% 下面的 targetTheta 也就是 小车当前航向与目标点的差值 (正数)
if goalTheta > theta
targetTheta = goalTheta-theta;%[deg]
else
targetTheta = theta-goalTheta;%[deg]
end
heading = 180 - targetTheta;
%% 计算动态窗口 model - 速度加速度等基本参数。 ok
% 返回 最小速度 最大速度 最小角速度 最大角速度速度
function Vr = CalcDynamicWindow(x,model)
V_SPD = 4;%机器人速度
W_ANGLE_SPD = 5;%机器人角速度
MD_MAX_V = 1;% 最高速度m/s]
MD_MAX_W = 2;% 最高旋转速度[rad/s]
MD_ACC = 3;% 加速度[m/ss]
MD_VW = 4;% 旋转加速度[rad/ss]
global dt;
% 车子速度的最大最小范围 依次为:最小速度 最大速度 最小角速度 最大角速度速度
Vs=[0 model(MD_MAX_V) -model(MD_MAX_W) model(MD_MAX_W)];
% 根据当前速度以及加速度限制计算的动态窗口 依次为:最小速度 最大速度 最小角速度 最大角速度速度
Vd = [x(V_SPD)-model(MD_ACC)*dt x(V_SPD)+model(MD_ACC)*dt ...
x(W_ANGLE_SPD)-model(MD_VW)*dt x(W_ANGLE_SPD)+model(MD_VW)*dt];
% 最终的Dynamic Window
Vtmp = [Vs;Vd]; % 2 X 4矩阵 每一列依次为:最小速度 最大速度 最小角速度 最大角速度速度
Vr = [max(Vtmp(:,1)) min(Vtmp(:,2)) max(Vtmp(:,3)) min(Vtmp(:,4))]; % 设定的参数 与 计算的速度 比较
%% Motion Model 根据当前状态推算下一个控制周期(dt)的状态。 oh!坐标变换的计算原理?
% u=[vt; wt];当前时刻的速度、角速度 x=状态[x(m),y(m),yaw(Rad),v(m/s),w(rad/s)]
function x = f(x, u)
global dt;
F = [1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 0 0
0 0 0 0 0];
B = [dt*cos(x(3)) 0
dt*sin(x(3)) 0
0 dt
1 0
0 1];
x= F*x+B*u; % 为何这样计算,暂不明白
% 弧度和角度之间的换算
%% degree to radian
function radian = toRadian(degree)
radian = degree/180*pi;
%% radian to degree
function degree = toDegree(radian)
degree = radian/pi*180;
%% END如图所示,绿线为机器人行驶的路径,红色椭圆为障碍物,机器人从左下角的起点运动到了右上角的终点。

该matlab程序中的“main.m” 为主程序,而“path_plan.m”则为算法的具体实现程序。
% -------------------------------------------------------------------------
% 人工势场算法
% 出处:GitHub-https://github.com/zzuwz/Artificial-Potential-Field
% 参考提供源代码作者提供的资料,依照个人理解,添加了大量中文注释
% —— 2021/10/29 Poaoz
% -------------------------------------------------------------------------
% 流程梳理 - 人工势场法
% 1)起点、终点、障碍物、迭代次数、取点半径等参数的设定
% 2)以起点为中心,作半径为r的圆,从圆上取八个均布的点
% 3)分别计算八个点的前进“代价”—— 终点对其的引力+所有障碍物对其的斥力
% 4)取“代价”最小的点的坐标,结合现有起点,计算得到新的起点,然后重复上述内容
% 5)当发现 一个点距离终点很近 or 迭代的次数计算完 程序停止。
%%
clc
clear
close all
figure(1);
axis([0 15 0 15]); % 地图 15x15
begin=[1;2]; % 起点
over=[14;13]; % 终点
obstacle=[5 8 10 7 10 5 ;5 6 9 9 13 10]; % 障碍物x;y坐标
% 绘制起点、终点、障碍物
hold on;
plot(begin(1),begin(2),'*b','MarkerSize',10);
plot(over(1),over(2),'*b','MarkerSize',10);
plot(obstacle(1,:),obstacle(2,:),'ob');
for i=1:size(obstacle,2) % 在个障碍物点处,绘制椭圆。 'Curvature' 矩形的曲率
rectangle('Position',[obstacle(1,i)-0.5,obstacle(2,i)-0.5,1,1],'Curvature',[1,1],'FaceColor','r');
end
point= path_plan(begin,over,obstacle); % 计算并绘制出路径% 算法梳理
% 1)起点、终点、障碍物、迭代次数、取点半径等的设定
% 2)以起点为中心,作半径为r的圆,均匀从圆上取八个点
% 3)分别计算八个点的前进“代价” 即 终点对其的引力+所有障碍物对其的斥力
% 4)取“代价”最小的点的坐标,结合现有起点,计算得到新的起点,然后重复上述内容
% 5)当发现 一个点距离终点很近 or 迭代的次数计算完了 程序停止。
% 该程序中,computP 负责代价计算,为核心计算函数。 可对其进行修改,以实现其他优化功能。
% 参数:起点 终点 障碍物 的坐标
% 返回值: point储存的一系列起点信息
function [ point ]= path_plan(begin,over,obstacle)
iters=1; % 迭代次数
curr=begin; % 起点坐标
testR=0.2; % 测试8点的圆的半径为0.5
while (norm(curr-over)>0.2) && (iters<=2000) % 未到终点&迭代次数不足
% attr=attractive(curr,over);
% repu=repulsion(curr,obstacle);
%curoutput=computP(curr,over,obstacle);
%计算当前点附近半径为0.2的8个点的势能,然后让当前点的势能减去8个点的势能取差值最大的,确定这个
%方向,就是下一步迭代的点
point(:,iters)=curr; % point为函数返回值,储存每次遍历得到的新起点 curr
%先求这八个点的坐标
for i=1:8 % 求 以curr为起点,testR为半径的圆上的八个均匀分布的点
testPoint(:,i)=[testR*sin((i-1)*pi/4)+curr(1);testR*cos((i-1)*pi/4)+curr(2)];
testOut(:,i)=computP(testPoint(:,i),over,obstacle); % 计算上述各个点的所受合力
end
[temp num]=min(testOut); % 找出这八个点中,代价最小的点
%迭代的距离为0.1
curr=(curr+testPoint(:,num))/2; % 将上述求得点,迭代到curr上。 (求取的 curr与testPoint 的中点)
plot(curr(1),curr(2),'og'); % 绘制得到的 新的起点curr
pause(0.01); % 程序暂停一会再继续运行 -- 体现出路径搜索的过程
iters=iters+1; % 迭代次数+1
end
end
% 计算周围几个点的势能(代价)
% 参数:当前起点 终点 障碍物 的坐标
function [ output ]= computP( curr,over,obstacle )
% 几个用于计算的相关参数
k_att=1;
repu=0;
k_rep=100;
Q_star=2; %。障碍物的斥力作用半径
% 计算终点对当前点的引力
% tips:这个数值越小,说明当前点离终点越近
attr=1/2*k_att*(norm(curr-over))^2; % 引力计算公式
% 计算所有障碍物对当前点斥力合
% tips:斥力合越小,说明当前点遇到障碍物的概率越小
for i=1:size(obstacle,2)
if norm(curr-obstacle(:,i))<=Q_star % 障碍物到当前点距离在阈值内,考虑其斥力影响
repu=repu+1/2*k_rep*(1/norm(curr-obstacle(:,i))-1/Q_star)^2; % 斥力计算公式
% ps: 当 curr和obstacle 坐标重合时,是否会出现repu计算卡死? 是否需要对该条件进行设置
else % 障碍物到当前点距离在阈值外,忽略斥力影响
repu=repu+0;
end
end
output=attr+repu; % 引力+斥力 这个数值越小,越适合当作下一个起点
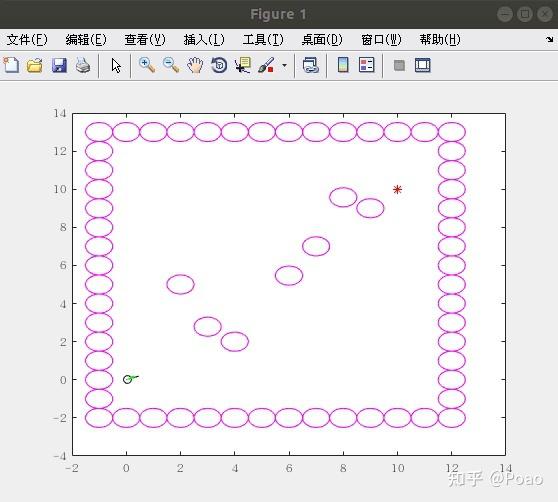
end 如图所示,两个矩形块为障碍物,蓝色树枝为算法搜索的过程演示,深蓝色小球路径为得到的最佳路径。(最佳路径由终点画线到起点)
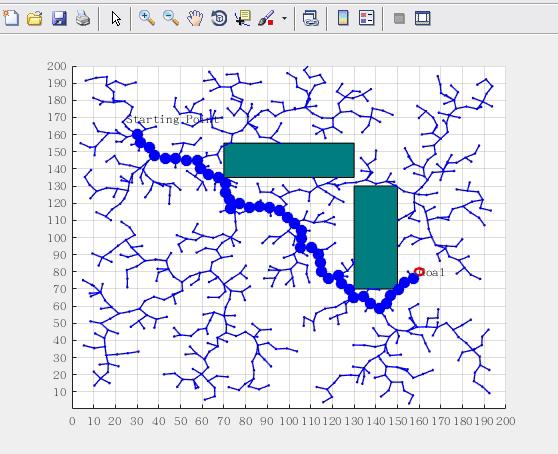
RRT算法文件夹也有两个m文件,其中"rrt_run.m"为主程序,其主要进行了相关参数及地图的初始化,具体的算法实现在“PlanPathRRTstar.m”文件当中。
% -------------------------------------------------------------------------
% RRT* 算法
% 出处:GitHub-https://github.com/wntun/RRT-star
% 参考提供源代码作者提供的资料,依照个人理解,添加了大量中文注释
% —— 2021/10/29 Poaoz
% -------------------------------------------------------------------------
% 流程梳理 - RRT算法
% 1) 进行起点、终点、障碍物、前进步长、迭代次数等参数的设定,rrt树的初始化
% 2) 在地图上随机采样一个点a,并找出现有节点中与其最近的节点b
% 3)沿最近的节点b到采样点a方向,根据机器人步长,求得新的节点c
% 4)对新的节点c进行障碍物判断 & 找到c的父节点 (最近点 or 可到达的点-eighbors)
% 5)如果新节点符合要求,将其插入到rrt树中(携带四个rrt参数) 并进行节点重连的路径优化计算
% 6)判断该新节点c是否“到达目标点”(按条件修改rrt的第四个参数),并持续重复上述“2-6”
% 7)迭代次数达到设定值后,根据得到的rrt树,找出最佳路径
function[]=rrt_run
% 画矩形块:[x,y,a,b]起始点(x,y),宽a,长b
function[]= rect(x,y,l,b)
hold on
rectangle('Position',[x,y,l,b],'FaceColor',[0 0.5 0.5])
end
% 画圆的函数
function circle(x,y,r)
ang=0:0.01:2*pi;
xp=r*cos(ang);
yp=r*sin(ang);
plot(x+xp,y+yp, '.r');
end
% 画图,及一些输入参数的设置
figure;
axis([0,200,0,200])
set(gca, 'XTick', 0:10:200)
set(gca, 'YTick', 10:10:200)
grid ON
hold on
% 画矩形块充当障碍物
rect(130,70,20,60); % 起点(130,70),右上角方向,宽20长60的矩形
rect(70,135,60,20); % 起点(70,135),右上角方向,宽60长20的矩形
p_start = [30;160]; % 起点,目标点设定
p_goal = [160;80];
rob.x = 30; % 机器人所在起点坐标
rob.y = 160;
% 初始化参数
param.obstacles =[130,70,20,60; 70,135,60,20;]; % 对应矩形块
param.threshold = 2;
param.maxNodes = 800;
param.step_size = 5; % 机器人每次行进步数
param.neighbourhood = 5; % 寻找子节点的距离
param.random_seed = 40;
plot(rob.x,rob.y,'.r')
text(rob.x-5, rob.y+9, 'Starting Point'); % 机器人的起点标识
% plot(p_goal(1), p_goal(2), '.r')
circle(p_goal(1), p_goal(2), 2) % 目标点画半径2的圆
text(p_goal(1), p_goal(2), 'Goal'); % 目标点标注文字
% 进行搜图并出结果
result = PlanPathRRTstar(param, p_start, p_goal)
endfunction result = PlanPathRRTstar(param, p_start, p_goal)
% RRT*
% credit : Anytime Motion Planning using the RRT*, S. Karaman, et. al.
% calculates the path using RRT* algorithm
% param : parameters for the problem
% 1) threshold : stopping criteria (distance between goal and current
% node)
% 2) maxNodes : maximum nodes for rrt tree
% 3) neighborhood : distance limit used in finding neighbors
% 4) obstacle : must be rectangle-shaped #limitation
% 5) step_size : the maximum distance that a robot can move at a time
% (must be equal to neighborhood size) #limitation
% 6) random_seed : to control the random number generation
% p_start :[x;y]coordinates
% p_goal :[x;y]coordinates
% variable naming : when it comes to describe node, if the name is with
% 'node', it means the coordinates of that node or it is just an index of
% rrt tree
% rrt struct : 1) p : coordinate, 2) iPrev : parent index, 3) cost :
% distance
% obstacle can only be detected at the end points but not along the line
% between the points 障碍物只能在端点处检测到,而不能沿着端点之间的直线检测到
% for cost, Euclidean distance is considered. 代价计算--欧几里得距离
% output : cost, rrt, time_taken
% whether goal is reached or not, depends on the minimum distance between
% any node and goal
% GitHub作者:GitHub-https://github.com/wntun/RRT-star
% 中文简述如下,给关系程序理解的大部分程序段都添加了注释。
% 部分细节可能存在偏差,望海涵。
% -- by Poaoz 2021/10/29
% 知乎:https://www.zhihu.com/people/panda-13-16
% 初始化参数简述 param
% 1) threshold : 停止搜索的距离阈值--当前节点于目标点的距离
% 2) maxNodes : RRT树的最大节点数
% 3) neighborhood : 父节点到下一个节点的步长
% 4) obstacle : 该程序的障碍物只能是矩形的,可通过修改函数【isObstacleFree(node_free)】替换其他的障碍物
% 5) step_size : 机器人一次可前进的步长,此处需与neighborhood相等
% 6) random_seed : 控制随机数生成的种子
% 代价计算说明: 采用norm计算两个坐标点之间的距离-欧几里得距离
% rrt 树参数结构简述
% 1) p : 节点坐标 pose
% 2) iPrev : 该节点的父节点索引 (rrt树中的索引) 联系了该节点与父节点
% 3) cost : 累计代价=父节点代价 + 父节点到该子节点的距离代价 【欧几里得距离】
% 4) goalReached : 是否到达目标点标志 (与设定的threshold有关)
% while循环进行的内容
% 1)地图上随机采样一个点
% 2)找出现有节点中,与该采样点最近的节点
% 3)沿最近的节点到采样点方向,根据机器人步长,求得新的节点
% 4)新节点的障碍物判断 & 找到新节点的父节点 (最近点 or 可到达的点neighbors_ind)
% 5)将新节点插入到rrt树中(非障碍物 & 四个rrt参数) 这里有 节点重连的路径优化
% 6)判断该节点是否满足阈值条件 “达到目标点”-threshold (第四个rrt参数)
% while循环结束后:根据得到到rrt树,计算出最终路径并绘制
% 最短路径寻找简述:
% 1)找出rrt中 goalReached=1 的节点
% 2)找出上述节点中,cost最小的节点(选一个就可)
% 3)根据该节点的rrt中第二个参数iPrev,找到其父节点
% 4)重新上述“3)”直到发现父节点为开始节点,便可得到一条cost最小的路径
% rrt树的四个参数
field1 = 'p';
field2 = 'iPrev'; % 借助该参数,可将整个路径搜索出来。
field3 = 'cost';
field4 = 'goalReached';
rng(param.random_seed); % 用指定的 randomseed 初始化随机数生成器
tic; % tic开始计时,常与toc配合使用,toc停止计时 (算法运行的时间计时)
start(); % 执行路径规划功能函数
function start()
% s=struct(field1,value1,...,fieldN,valueN) 创建一个包含多个字段的结构体数组
rrt(1) = struct(field1, p_start, field2, 0, field3, 0, field4, 0);
N = param.maxNodes; % 迭代次数 iterations
j = 1;
% while endcondition>param.threshold %&& j<=N
% 每走一次循环,j++,一共循环N次
while j<=N
% 1)随机采样一个点
sample_node = getSample();
% plot(sample_node(1), sample_node(2), '.g');
% text(sample_node(1), sample_node(2), strcat('random',num2str(j)))
% 2)找到现有节点中,距离该采样点最近的点
nearest_node_ind = findNearest(rrt, sample_node);
% plot(rrt(nearest_node_ind).p(1), rrt(nearest_node_ind).p(2), '.g');
% text(rrt(nearest_node_ind).p(1), rrt(nearest_node_ind).p(2), strcat('nearest', num2str(j)));
% 3)沿最近点到采样点方向,按照步长前进,得到新的节点
new_node = steering(rrt(nearest_node_ind).p, sample_node);
if (isObstacleFree(new_node)==1) % 4.1) 新节点的障碍物检测
% plot(new_node(1), new_node(2), '.g');
% text(new_node(1), new_node(2)+3, strcat('steered: new node', num2str(j)))
% 获取新节点附近可到达的节点索引 neighbourhood
neighbors_ind = getNeighbors(rrt, new_node);
if(~isempty(neighbors_ind)) % 4.2) 判断附近可达到的节点 存在与否 (找该新节点的父节点)
% 存在— 从根节点为新子节点选择成本最低的父节点 【难理解1】
parent_node_ind = chooseParent(rrt, neighbors_ind, nearest_node_ind,new_node);
% plot(rrt(parent_node_ind).p(1), rrt(parent_node_ind).p(2), '.g');
% text(rrt(parent_node_ind).p(1), rrt(parent_node_ind).p(2)+3, strcat('parent', num2str(j)));
else
% 不存在— 选取距离该采样点最近的点为父节点
parent_node_ind = nearest_node_ind;
end
% 5)将新节点插入到 rrt搜索树中
rrt = insertNode(rrt, parent_node_ind, new_node);
if (~isempty(neighbors_ind)) % 存在可到达节点时,进行重连操作 优化路径 【难理解2】
rrt = reWire(rrt, neighbors_ind, parent_node_ind, length(rrt));
end
% 满足距离阈值条件,记该节点为到达目标 (但依旧会持续嵌套搜索)
if norm(new_node-p_goal) == param.threshold
rrt = setReachGoal(rrt);
end
end
j = j + 1;
end
setPath(rrt); % 上述while结束后,绘制寻找的路径
% text1=strcat('Total number of generated nodes:', num2str(j-1))
% text1=strcat('Total number of nodes in tree:', length(rrt))
end
%% 一系列功能函数(start中调用)
% 在rrt树中标记该节点为“到达目标点”(第四个参数) ok
function rrt=setReachGoal(rrt)
rrt(end).goalReached = 1;
end
% 绘制出 rrt中各个节点的关系,并标识出最终得到的路径 ok
function setPath(rrt)
% 1)绘制rrt树 :各个父节点与子节点之间的连线 【父节点→子节点】
for i = 1: length(rrt)-1
p1 = rrt(i).p; % 遍历rrt中各个节点
rob.x = p1(1); rob.y=p1(2);
plot(rob.x,rob.y,'.b') % 绘制各个节点
child_ind = find([rrt.iPrev]==i); % 寻找rrt中父节点索引为i的一堆子节点
for j = 1: length(child_ind) % 遍历上述一堆子节点
p2 = rrt(child_ind(j)).p; % 找到并绘制 上述父节点到子节点 的连线
pause(0.01); % 程序暂停一会再继续运行 -- 体现出路径搜索的过程
plot([p1(1),p2(1)], [p1(2),p2(2)], 'b', 'LineWidth', 1);
end
end
% 2)找到最短路径,并绘制
[cost,i] = getFinalResult(rrt);
result.cost = cost;
result.rrt = [rrt.p]; % result输出的节点坐标
% 绘制最终得到的最短路径
while i ~= 0
p11 = rrt(i).p;
plot(p11(1),p11(2),'b', 'Marker','.', 'MarkerSize', 30);
i = rrt(i).iPrev;
if i ~= 0
p22 = rrt(i).p; % 依次画出该节点,其父节点,其父节点的父节点(从终点画到起点)
plot(p22(1),p22(2),'b', 'Marker', '.', 'MarkerSize', 30);
pause(0.02); % 程序暂停一会再继续运行 -- 体现出路径搜索的过程
% plot([p11(1),p22(1)],[p11(2),p22(2)], 'b', 'LineWidth', 3);
end
end
result.time_taken = toc; % 返回程序总的运行时间
end
% 找最终路径 (在setPath中调用) ok
% 参 数:rrt树
% 返 回 值:代价cost 最接近终点的最优节点索引
% 寻找方法:寻找“到达目标点”的节点中,代价最小的节点
% 由该代价最小的节点,rrt树中的第二个参数iPrev,可再找到其父节点,由此可得到一条代价最小的路径
function [value,min_node_ind]= getFinalResult(rrt)
% 找到所有“到目标点”的节点索引 rrt第四个参数
goal_ind = find([rrt.goalReached]==1);
if ~(isempty(goal_ind)) % 判断是否达到目标点(goal是否存在)
disp('Goal has been reached!');
rrt_goal = rrt(goal_ind); % 储存“到目标点”节点
value = min([rrt_goal.cost]); % 取得上述节点中 cost最小值
min_node_ind = find([rrt.cost]==value); % 找到 cost最小值节点的索引
if length(min_node_ind)>1 % 如果cost最小值对应的索引有多个,取第一个即可
min_node_ind = min_node_ind(1);
end
else % goal_ind不存在
disp('Goal has not been reached!');
% 计算rrt中各个节点到目标点的距离,求出最小的一个节点,充当“终点”
for i =1:length(rrt)
norm_rrt(i) = norm(p_goal-rrt(i).p);
end
[value,min_node_ind]= min(norm_rrt); % 求取其中距离目标点最近的节点
value = rrt(min_node_ind).cost; % 以求得的该点信息作为返回值
end
end
% 新节点的障碍物判断函数 (针对此程序的矩形障碍物判断) ok
% 参 数:新节点的坐标信息
% 返 回 值: 0-有障碍物 1-无障碍物
% 判断方法:节点坐标是否在矩形障碍物四个端点的约束内(可更改该函数,实现障碍物的不同变换)
% param.obstacles=[130,70,20,60; 70,135,60,20;];
function free=isObstacleFree(node_free)
free = 1;
for i = 1: length(param.obstacles(:,1))
obstacle = param.obstacles(i,:); % 取一个矩形障碍物的信息
op1 = [obstacle(1), obstacle(2)]; % 根据信息求得矩形的四个端点坐标
op2 = [op1(1)+obstacle(3), op1(2)];
op3 = [op2(1), op1(2) + obstacle(4)];
op4 = [op1(1), op3(2)];
nx = node_free(1); % 取得待判断节点的xy坐标
ny = node_free(2);
% 判断节点是否在障碍物范围内
if ((nx>=op1(1) && nx<=op2(1)) && (ny>=op1(2) && ny<=op4(2)))
free = 0;
end
end
end
% 【step_size】 ok
% 沿最近点到采样点方向,按照机器人步长前进,得到新的节点
% 参 数: 离采样点最近的节点 采样点
% 返 回 值: 新节点的坐标
function new_node=steering(nearest_node, random_node)
dist = norm(random_node-nearest_node); % 两点距离
ratio_distance = param.step_size/dist;
% 计算新节点的xy坐标 (这里也可使用其他方式进行计算)
x = (1-ratio_distance).* nearest_node(1)+ratio_distance .* random_node(1);
y = (1-ratio_distance).* nearest_node(2)+ratio_distance .* random_node(2);
new_node = [x;y];
end
% 范围内的可到达的节点重新连接,以得到更优的路径
% 参 数: rrt树 临近节点索引 父节点索引 新节点的索引--rrt节点总数(前面传入)
% 返 回 值: 更新 新节点附近的临近节点的 父节点 【建立了更短的路径联系】
function rrt = reWire(rrt, neighbors, parent, new)
for i=1:length(neighbors) % 遍历每个可达到的临近节点
cost = rrt(new).cost + norm(rrt(neighbors(i)).p - rrt(new).p); % 求以新节点作为父节点时,临近节点的代价
if (cost<rrt(neighbors(i)).cost) % 如果 上述新代价 小于 临近节点现有代价
% if norm(rrt(new).p-rrt(neighbors(i)).p)<param.step_size
% % plot(rrt(neighbors(i)).p(1), rrt(neighbors(i)).p(2), '.b');
% rrt(neighbors(i)).p=steering(rrt(new).p, rrt(neighbors(i)).p);
% end
% plot(rrt(neighbors(i)).p(1), rrt(neighbors(i)).p(2), '.m');
rrt(neighbors(i)).iPrev = new; % 将 新节点作为 该临近节点的 父节点
rrt(neighbors(i)).cost = cost;
end
end
end
% 将新的节点插入rrt树末尾 ok
% 参 数: rrt 父节点索引 新节点坐标
% 返 回 值: 更新rrt
% 其中第三个参数 cost=父节点代价+新节点到父节点的代价
function rrt = insertNode(rrt, parent, new_node)
rrt(end+1) = struct(field1, new_node, field2, parent, field3, rrt(parent).cost + norm(rrt(parent).p-new_node), field4, 0);
end
% 从根节点为新子节点选择成本最低的父节点 ok 父节点?
% 参 数: rrt 临近的节点 最近的节点 新节点
% 返 回 值: 父节点索引
function parent = chooseParent(rrt, neighbors, nearest, new_node)
min_cost = getCostFromRoot(rrt, nearest, new_node); % 求以最近的节点为父节点时,新节点的代价
parent = nearest; % 暂取最近的节点,作为父节点
for i=1:length(neighbors) % neighbors - 下一步可到达的节点
cost = getCostFromRoot(rrt, neighbors(i), new_node); % 求以可到达的节点为父节点时,新节点的代价
if (cost<min_cost) % 最终取代价最小的那个节点,作为父节点
min_cost = cost;
parent = neighbors(i);
end
end
end
% 父节点的cost + 子节点到父节点的距离代价 ok
% 参 数: rrt 父节点索引 子节点
% 返 回 值: 子节点的代价
function cost = getCostFromRoot(rrt, parent, child_node)
cost = rrt(parent).cost + norm(child_node - rrt(parent).p);
end
% 【neighbourhood】 ok
% 获取指定节点周围可以到达的节点索引
% 参 数: rrt node -new_node(上面调用时传的参数)
% 返 回 值: 保存可到达节点的索引的neighbors
function neighbors = getNeighbors(rrt, node)
neighbors = [];
for i = 1:length(rrt) % 遍历rrt树中所有的节点
dist = norm(rrt(i).p-node); % 计算rrt中各个节点到node的距离代价
if (dist<=param.neighbourhood) % 找到 距离代价<单次行进步长的节点索引
neighbors = [neighbors i]; % 使用 neighbors 将节点索引保存
end
end
end
% 在坐标图上生成随机的采样点 ok
function node = getSample()
x = 0;
y = 0;
a = 0;
b = 200;
node = [x;y];
node(1) = (b-a) * rand(1) + a;
node(2) = (b-a) * rand(1) + a;
end
% 寻找rrt树中距离采样点最近的节点 ok
function indx = findNearest(rrt, n)
mindist = norm(rrt(1).p - n);
indx = 1;
for i = 2:length(rrt)
dist = norm(rrt(i).p - n);
if (dist<mindist)
mindist = dist;
indx = i;
end
end
end
end图中,蓝色为障碍物、绿色为起点、红色为终点、黑线为最短路径。
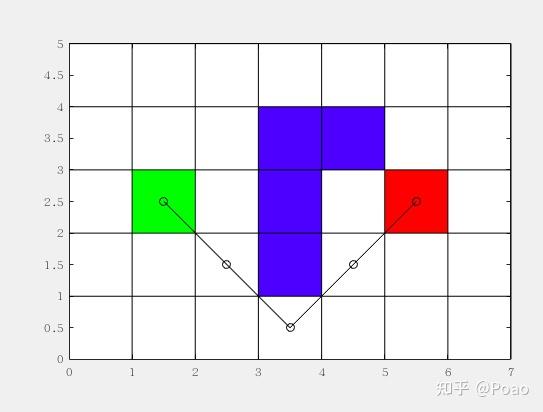
Astar算法文件夹也有两个m文件,其中"star.m"为主程序,其主要进行了相关参数及地图的初始化、openlist和closelist的更新、路径的寻找等,而“child_nodes_cal.m”文件进行的内容只是寻找父节点四面八方这八个位置中可选择的子节点,以便进行后续的代价计算。
% -------------------------------------------------------------------------
% A*算法
% 出处:https://b23.tv/5mMqX1 - b站up主【小黎的Ally】
% 视频教程中讲解大部分内容,但closeList_path\\openList_path没怎么说
% 为此,根据个人理解添加了 —— 2021/10/27 Poaoz
% -------------------------------------------------------------------------
% 流程梳理 - A*算法
% 1)起点、终点、障碍物等参数的设定 & openlist、closelist的初始化
% 2)从起点出发,将起点作为父节点,记录起点到父节点的路径
% 3)对父节点周围的八个点进行障碍物判断,找出可前进的子节点
% 4)挨个计算上述子节点的代价,记录【起点到其父节点,再到该子节点的路径】,并将其放到openlist中
% 5)将父节点(包括起点到父节点的路径)移动到closelist中,然后从openlist中寻找一个代价最小的节点,作为下一步的父节点
% 6)对该新的父节点,重复上述“3-5”,直到发现 新的父节点就是目标节点
% 7)从closelist取出最后一行,其第一个元素为目标点坐标,第二个元素为【起点到目标点的最优路径--- 一串坐标值】
clc
clear
close all
%% 建立地图
% m行 n列的网格 5 7
m = 5;
n = 7;
start_node = [2, 3]; % 起点
target_node = [6, 3]; % 终点
obs = [4,2; 4,3; 4,4 ;5,4]; % 障碍物
% 画xy的网格直线
for i = 1:m
plot([0,n], [i, i], 'k');
hold on
end
for j = 1:n
plot([j, j], [0, m], 'k');
end
axis equal
xlim([0, n]);
ylim([0, m]);
% 使用fill命令,将起点、终点、障碍物 染色
% fill([x1,x2,x3,x4],[y1,y2,y3,y4],'k')
% 按照顺序连接四点 x1,y1 x2,y2 ,,, x4,y4, 然后填充封闭图形
fill([start_node(1)-1, start_node(1), start_node(1), start_node(1)-1],...
[start_node(2)-1, start_node(2)-1 , start_node(2), start_node(2)], 'g');
fill([target_node(1)-1, target_node(1), target_node(1), target_node(1)-1],...
[target_node(2)-1, target_node(2)-1 , target_node(2), target_node(2)], 'r');
for i = 1:size(obs,1) % size求出obs的行数
temp = obs(i,:); % obs的某一行
fill([temp(1)-1, temp(1), temp(1), temp(1)-1],...
[temp(2)-1, temp(2)-1 , temp(2), temp(2)], 'b');
end
%% openlist closelist的建立
% close 储存最近点, open 储存已经计算过的点(去除close)
% xxxxList_path 的格式[[x1,y1],[x1,y1;x2,y2];[x2,y2],[x1,y1;x2,y2;...]...]
% xxxxList_path{i,1}-某个节点坐标;_path{i,2}-从出发点到该节点的路径
% 关于path的内容,可运行一遍程序后,于【工作区】查看对应两个变量的具体内容
% closeList
closeList = start_node;
closeList_path = {start_node,start_node};
closeList_cost = 0;
child_nodes = child_nodes_cal(start_node, m, n, obs, closeList); % 计算下一步需要计算的子节点
% openList 节点、路径、代价
openList = child_nodes; % 拷贝待计算的子节点[x,y; xx,yy; xxx,yyy....]
for i = 1:size(openList,1)
openList_path{i,1} = openList(i,:); % 节点坐标
openList_path{i,2} = [start_node;openList(i,:)]; % 从出发点到该节点
end
% 求取f=g+h g父节点到子节点 h子节点到目标
for i = 1:size(openList, 1)
g = norm(start_node - openList(i,1:2)); % norm(v) 求欧几里德长度-向量模 1&根号二
h = abs(target_node(1) - openList(i,1)) + abs(target_node(2) - openList(i,2)); % 求xxx距离
f = g + h; % 总代价
openList_cost(i,:) = [g, h, f]; % 各子节点代价赋值储存
end
%%
% 寻找openList中总代价f最小的节点,并将其作为下一个父节点
[~, min_idx] = min(openList_cost(:,3));
parent_node = openList(min_idx,:);
%% 循环搜索
% 找到父节点,计算其周围的子节点并将其加入openlist;然后将父节点移动到closelist中,并寻找新的“父节点”
% 如此往复,直到新找到的父节点是目标点。
% 整个过程中,会记录 a-【从起点到父节点的路径】 b-【起点到父节点再到子节点的路径】
% 而每次寻找新的父节点时,会将a移动到close中,并从b中选一个作为下一次的“a”
flag = 1;
while flag
% 寻找下一步的子节点
child_nodes = child_nodes_cal(parent_node, m, n, obs, closeList);
% 判断子节点是否在openList:在则更新其代价值,不在则加到openlist中
for i = 1:size(child_nodes,1)
child_node = child_nodes(i,:);
% in_flag-是否在openlist中 openList_idx-在openlist的哪个位置
[in_flag,openList_idx] = ismember(child_node, openList, 'rows');
% g=到父节点的距离g + 父节点到子节点距离
g = openList_cost(min_idx, 1) + norm(parent_node - child_node);
h = abs(child_node(1) - target_node(1)) + abs(child_node(2) - target_node(2));
f = g+h;
% path补充:openList_path{min_idx,2}即【出发点到当前父节点】的路径
% 因为当前父节点是最短代价,故该路径算是目前的最短代价
if in_flag % 子节点在openlist中 (是否更优的路径)
if g < openList_cost(openList_idx,1) % 如果现在的g值 小于 已经存在的该节点的g值
openList_cost(openList_idx, 1) = g; % 更新该节点的代价值
openList_cost(openList_idx, 3) = f;
openList_path{openList_idx,2} = [openList_path{min_idx,2}; child_node];
end
else % 不在,将子节点加入openList末尾
openList(end+1,:) = child_node;
openList_cost(end+1, :) = [g, h, f];
openList_path{end+1, 1} = child_node; % path中加入节点
openList_path{end, 2} = [openList_path{min_idx,2}; child_node]; % 更新该节点路径为【出发到该节点】
end
end
% 将openList中上述父节点移动到 closeList中(非刚刚更新的openlist中代价最小的节点)
closeList(end+1,: ) = openList(min_idx,:);
closeList_cost(end+1,1) = openList_cost(min_idx,3);
closeList_path(end+1,:) = openList_path(min_idx,:);
openList(min_idx,:) = []; % 从openlist清除该父节点
openList_cost(min_idx,:) = [];
openList_path(min_idx,:) = [];
% 寻找openList中总代价最小的节点,并将其作为下一个父节点(刚更新的openlist)
[~, min_idx] = min(openList_cost(:,3));
parent_node = openList(min_idx,:);
% 父节点为目标,停止搜索
if parent_node == target_node % 加入到closelist中
closeList(end+1,: ) = openList(min_idx,:);
closeList_cost(end+1,1) = openList_cost(min_idx,1);
closeList_path(end+1,:) = openList_path(min_idx,:); % 将从起点到目标点的路径移动至close中
flag = 0; % 退出循环
end
end
%% 画出路径
path_opt = closeList_path{end,2}; % 取数组中最后一行的第二个元素为路径
path_opt(:,1) = path_opt(:,1)-0.5; % 散点为各个方块中心点,故需进行坐标偏移
path_opt(:,2) = path_opt(:,2)-0.5;
scatter(path_opt(:,1), path_opt(:,2), 'k'); % 画一系列散点
plot(path_opt(:,1), path_opt(:,2), 'k'); % 将散点们连线
%% 判断父节点周围的八个点是否为需进行计算的子节点
function child_nodes = child_nodes_cal(parent_node, m, n, obs, closeList)
child_nodes = [];
field = [1,1; n,1; n,m; 1,m]; % 矩形地图区域的四个点
% 左上 ↖?
child_node = [parent_node(1)-1, parent_node(2)+1]; % 子节点坐标
% inpolygon(xq,yq,xv,yv)命令,查询xq,yq是否在xv,yv定义的多边形区域内 (:,i)列向量
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
% 判断 child_nodes 是否与 obs 有相同的行。
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node]; % 该点不在obs中,将其加入子节点
end
end
% 上
child_node = [parent_node(1), parent_node(2)+1];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 右上 ↗?
child_node = [parent_node(1)+1, parent_node(2)+1];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 左
child_node = [parent_node(1)-1, parent_node(2)];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 右
child_node = [parent_node(1)+1, parent_node(2)];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 左下 ↙?
child_node = [parent_node(1)-1, parent_node(2)-1];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 下
child_node = [parent_node(1), parent_node(2)-1];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
% 右下 ↘?
child_node = [parent_node(1)+1, parent_node(2)-1];
if inpolygon(child_node(1), child_node(2), field(:,1), field(:,2))
if ~ismember(child_node, obs, 'rows')
child_nodes = [child_nodes; child_node];
end
end
%% 删除已经在closeList中的子节点
delete_idx = [];
for i = 1:size(child_nodes, 1)
if ismember(child_nodes(i,:), closeList , 'rows')
delete_idx(end+1,:) = i;
end
end
child_nodes(delete_idx, :) = [];






